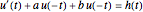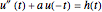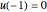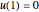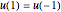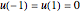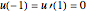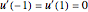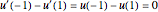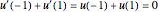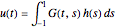Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Green's Functions with Reflection Conditions

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

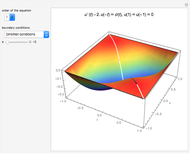
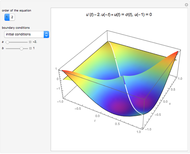
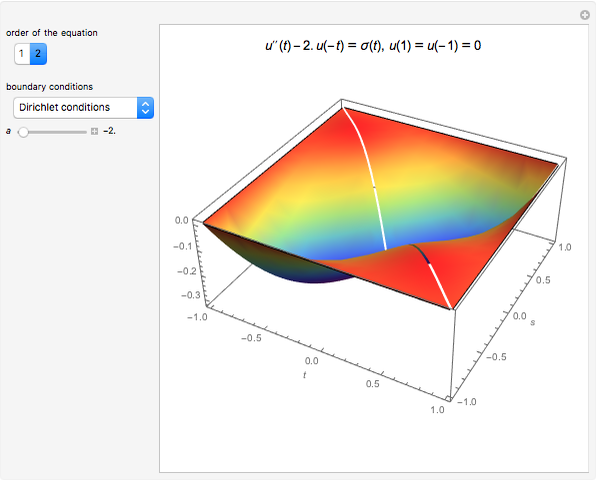
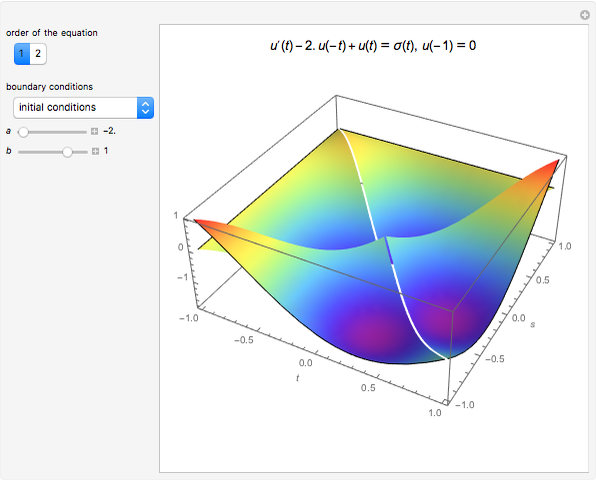
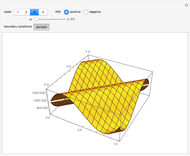
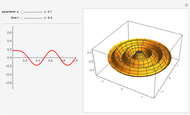
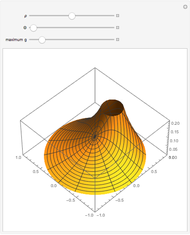
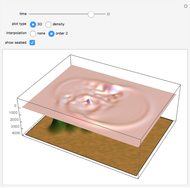
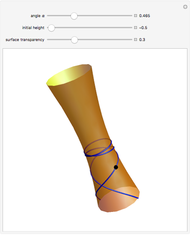
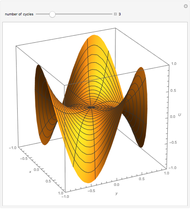
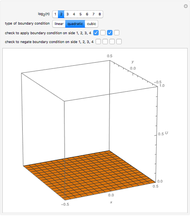
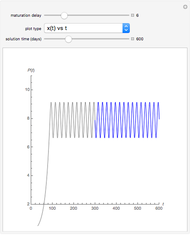
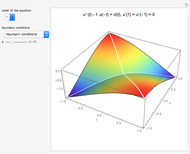
This Demonstration plots the Green’s function for the linear differential equation with reflection of order 1,

[more]

,

and order ,

,

where you can vary the parameters and . These equations are coupled with one of the following linear boundary conditions:

Order 1:

initial condition: ,

final condition: ,

periodic condition: ,

antiperiodic conditions: .

Order 2:

Dirichlet conditions: ,

mixed conditions: ,

Neumann conditions: ,

periodic conditions: ,

antiperiodic conditions: ,

The solution of the boundary value problem (differential equation and boundary conditions) is given by .

In the code, the expression for the corresponding Green’s function is given for the arbitrary interval .

[less]

Contributed by: Alberto Cabada, José Ángel Cid, F. Adrián F. Tojo, and Beatriz Máquez-Villamarín (December 2014)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The way to compute a Green's function for a problem with reflection is described in [1].

You can download a notebook for computing other Green's functions with reflection from [2].

References

[1] A. Cabada and F. Adrián F. Tojo, "An Algebraic Method of Obtaining the Green's Function for Some Reducible Functional Differential Equations." arxiv.org/abs/1411.5507.

[2] F. Adrián F. Tojo, A. Cabada, J. A. Cid, and B. Máquez-Villamarín, "Green's Functions with Reflection" from Wolfram Library Archive—A Wolfram Web Resource. library.wolfram.com/infocenter/MathSource/9087.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send