Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

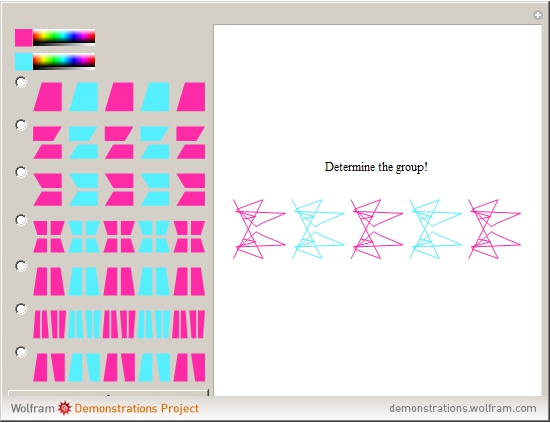
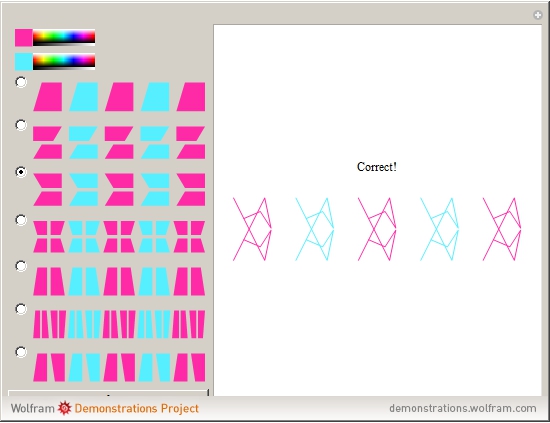
Guess the Antisymmetric Frieze Group, Part 1

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

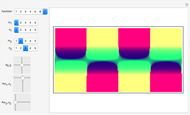
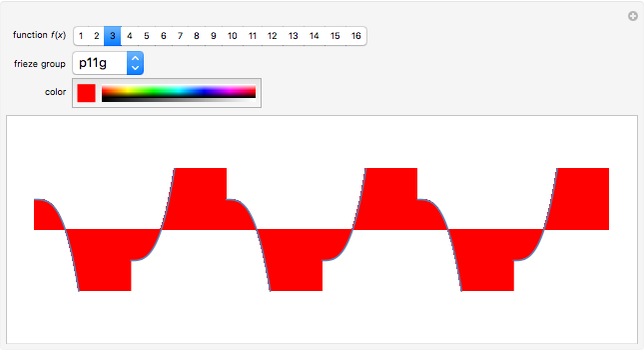
A frieze is a design on a two-dimensional strip that is periodic along the strip. These are often found in decorative art and in architectural design. Taking into account all possible symmetries (by translations, reflections, and rotations), seven classes of frieze groups are possible.

[more]

An antisymmetric frieze group, using color-change translation, is shown in the right panel. Try to match this with the corresponding design in the control panel, until you get a message that your choice is correct.

[less]

Contributed by: Izidor Hafner (January 2016)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Reference

[1] L. Radovic and S. Jablan, "Antisymmetry and Modularity in Ornamental Art," in Proceedings of Bridges: Mathematical Connections in Art, Music, and Science, Kansas, 2001 pp. 55–66. archive.bridgesmathart.org/2001/bridges2001-55.pdf.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send