Hamilton-Connected Harary Graphs

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The Harary graphs 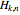 are a specifically defined family of graphs on
are a specifically defined family of graphs on  vertices that are
vertices that are  -connected and have the minimum possible number of edges for such a graph,
-connected and have the minimum possible number of edges for such a graph, 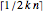 . A path is Hamiltonian if it visits all vertices without repetition. This Demonstration illustrates a proof that
. A path is Hamiltonian if it visits all vertices without repetition. This Demonstration illustrates a proof that 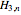 , where
, where  has the form
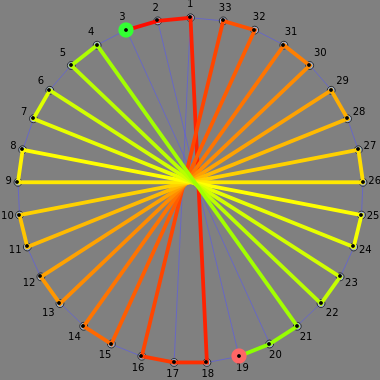
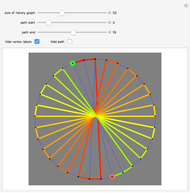
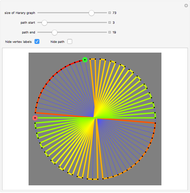
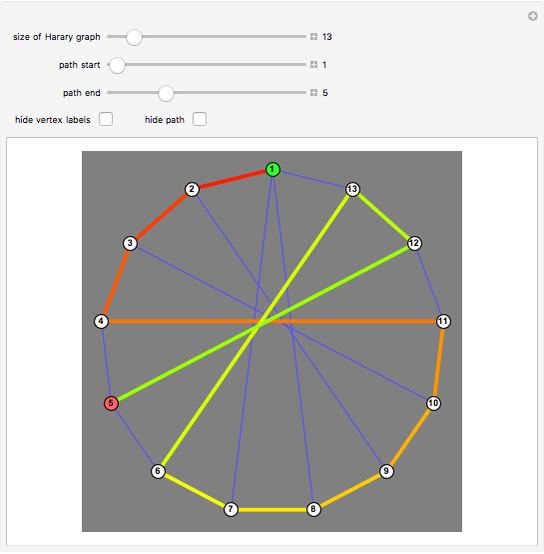
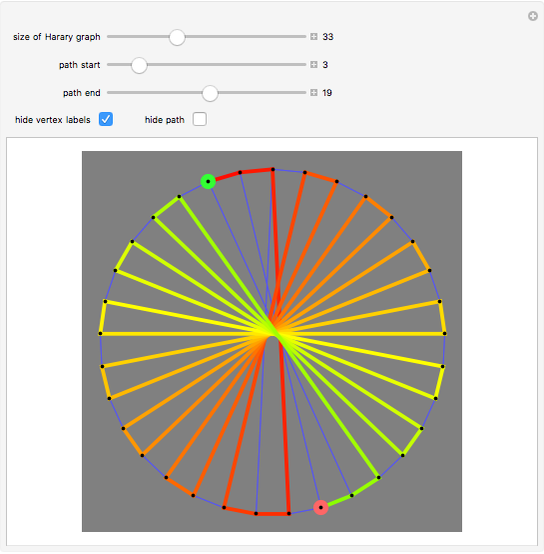
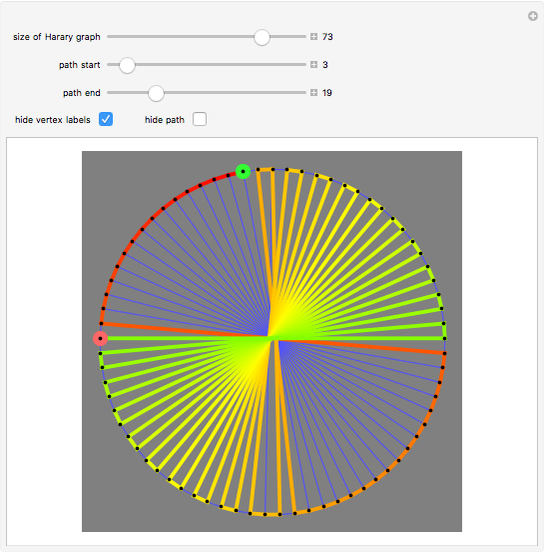
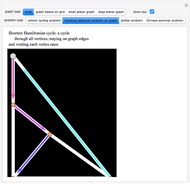
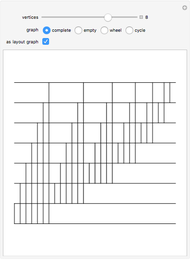
has the form  , admits a Hamiltonian path from any vertex to any other. (The start vertex is green and end vertex is red.)
, admits a Hamiltonian path from any vertex to any other. (The start vertex is green and end vertex is red.)
Contributed by: Stan Wagon (March 2013)
(Macalester College)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A graph is Hamilton-connected if, for any vertices 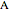 and
and 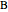 , there is a Hamiltonian path from
, there is a Hamiltonian path from 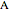 to
to 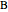 . In most cases the Harary graphs are circulants, or have a circulant as an edge subgraph (see [1] or [4] for the explicit construction). For example, if
. In most cases the Harary graphs are circulants, or have a circulant as an edge subgraph (see [1] or [4] for the explicit construction). For example, if  is even or
is even or  is even, then
is even, then 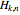 is a circulant graph. And if
is a circulant graph. And if  is odd, then
is odd, then 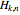 has a circulant as an edge subgraph. When
has a circulant as an edge subgraph. When 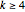 , the circulants that arise are connected, not bipartite, and not a cycle, and therefore the Chen–Quimpo theorem [2] on Hamilton-connectedness of such circulants applies: such graphs are Hamilton-connected.
, the circulants that arise are connected, not bipartite, and not a cycle, and therefore the Chen–Quimpo theorem [2] on Hamilton-connectedness of such circulants applies: such graphs are Hamilton-connected.
The case 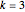 is different, because the circulant graphs that underlie the Harary graphs are not all Hamilton-connected.
is different, because the circulant graphs that underlie the Harary graphs are not all Hamilton-connected.
• 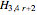 is a bipartite circulant and so is not Hamilton-connected, though it is Hamilton-laceable, by the Chen–Quimpo theorem.
is a bipartite circulant and so is not Hamilton-connected, though it is Hamilton-laceable, by the Chen–Quimpo theorem.
• 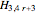 can be proved to be not Hamilton-connected: there is no path from the unique vertex of maximum degree to the vertex two steps away in the natural circular order.
can be proved to be not Hamilton-connected: there is no path from the unique vertex of maximum degree to the vertex two steps away in the natural circular order.
• 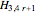 is the reason for this Demonstration, which shows the paths that arise in a proof that these graphs are Hamilton-connected. There are several different cases based on the parity of the starting vertex and the position of the target vertex.
is the reason for this Demonstration, which shows the paths that arise in a proof that these graphs are Hamilton-connected. There are several different cases based on the parity of the starting vertex and the position of the target vertex.
References
[1] O. Baudon, J. Bensmail, E. Sopena, "Partitioning Harary Graphs into Connected Subgraphs Containing Prescribed Vertices," preprint. hal.inria.fr/docs/00/68/99/34/PDF/bbs2012.pdf.
[2] C. C. Chen and N. F. Quimpo, "On Strongly Hamiltonian Abelian Group Graphs," Lecture Notes in Mathematics, Vol. 884, (K. L. McAvaney, ed.), Berlin: Springer-Verlag, 1981 pp. 23–34. link.springer.com/chapter/10.1007%2 FBFb0091805.
[3] F. Harary, "The Maximum Connectivity of a Graph," Proceedings of the National Academy of Science, 48(7), 1962 pp. 1142–1146. www.jstor.org/stable/71730.
[4] D. B. West, Introduction to Graph Theory, 2nd ed., Upper Saddle River, NJ: Prentice-Hall, 2001 pp. 150–151.
Permanent Citation