Heat Diffusion in a Semi-Infinite Region

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
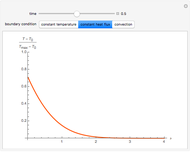
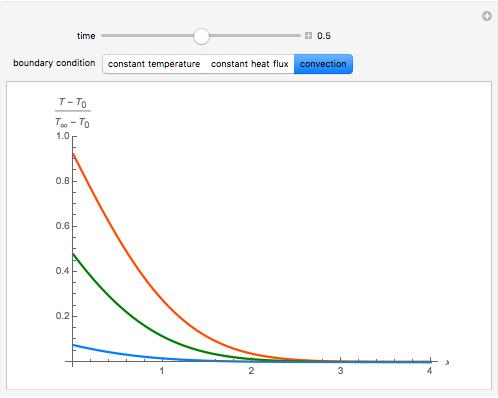
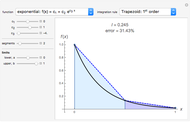
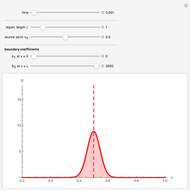
This Demonstration shows solutions for the one-dimensional heat diffusion equation 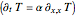 in a semi-infinite region. Starting from a uniform initial temperature,
in a semi-infinite region. Starting from a uniform initial temperature, 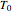 , and using normalized parameters (
, and using normalized parameters (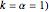 , the dimensionless temperature distribution is animated in time for the three classical boundary conditions at
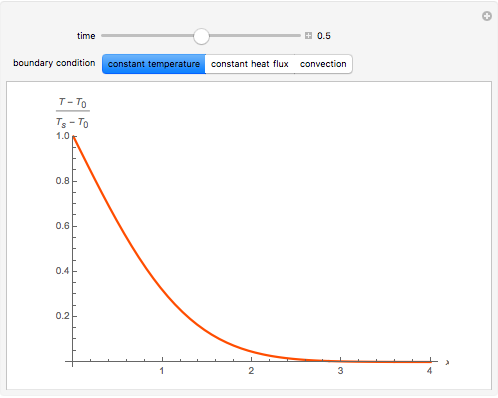
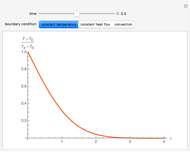
, the dimensionless temperature distribution is animated in time for the three classical boundary conditions at  , namely: constant surface temperature,
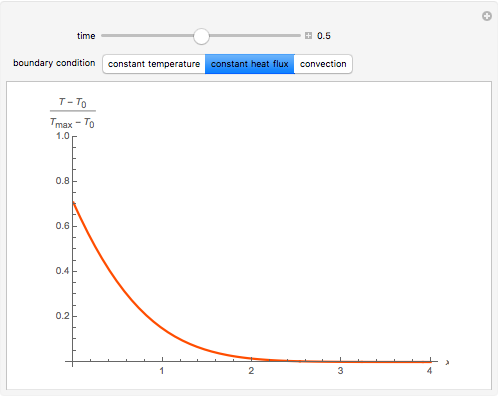
, namely: constant surface temperature, 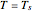 ; constant surface heat flux,
; constant surface heat flux, 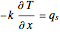 ; and convective exchange with a fluid at
; and convective exchange with a fluid at 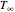 ,
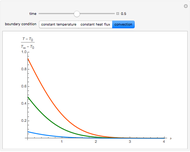
, 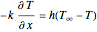 . For the convection case, temperature distributions for a relatively high, medium, and low value of the heat transfer coefficient
. For the convection case, temperature distributions for a relatively high, medium, and low value of the heat transfer coefficient  are displayed. A high
are displayed. A high  (red curve) gives results close to the constant surface temperature case, while a low
(red curve) gives results close to the constant surface temperature case, while a low  value (blue curve) gives results similar to the constant heat flux case. In all cases the thermal affected zone is of the order of
value (blue curve) gives results similar to the constant heat flux case. In all cases the thermal affected zone is of the order of  .
.
Contributed by: Brian Vick (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
These animations were generated from the analytical solutions, which can be found in the source code. The following nomenclature is used.
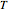 = temperature (K)
= temperature (K)
 = position (m)
= position (m)
 = time (s)
= time (s)
 = thermal conductivity (W/m K)
= thermal conductivity (W/m K)
 = thermal conductivity (W/m
= thermal conductivity (W/m 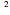 )
)
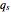 = surface heat flux (W/m
= surface heat flux (W/m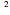 )
)
 = heat transfer coefficient (W/m
= heat transfer coefficient (W/m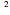 K)
K)
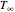 = external fluid temperature (K)
= external fluid temperature (K)
Permanent Citation