Heat Transfer and Temperature Distribution in a Fin

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
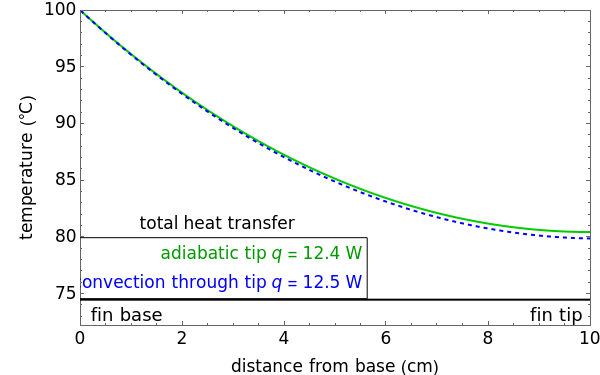
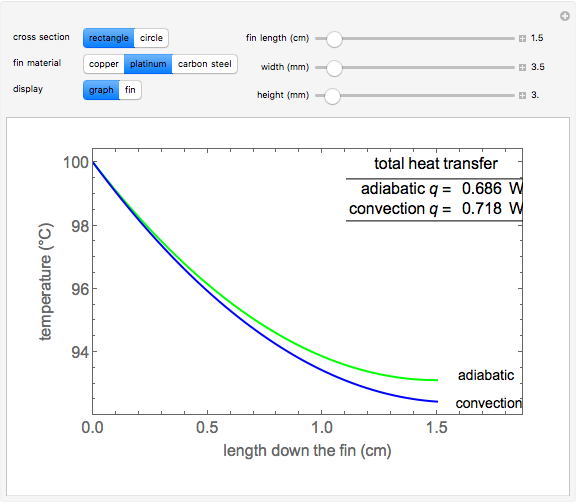
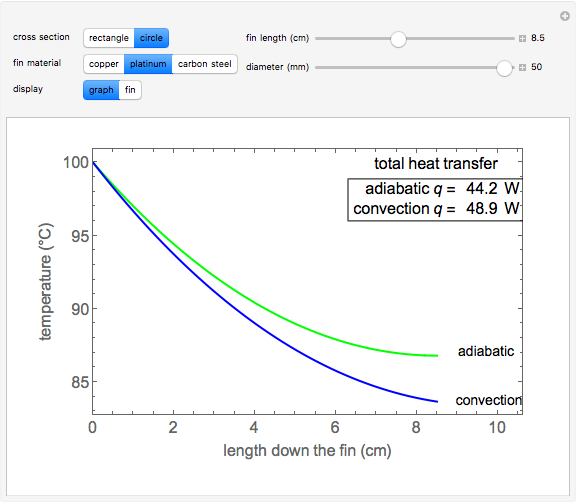
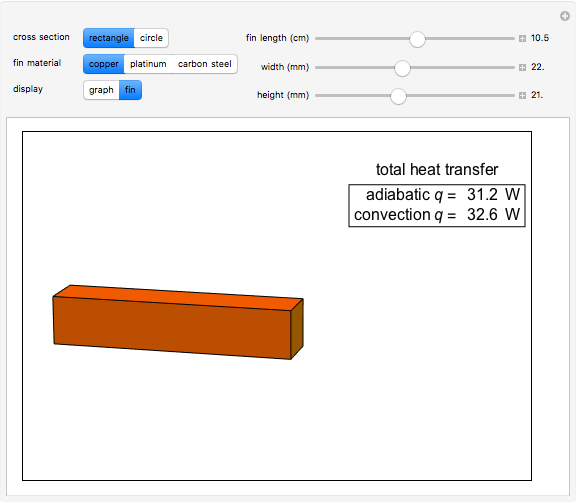
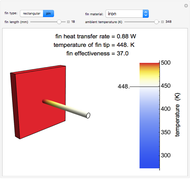
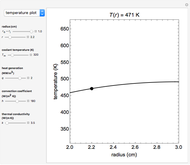
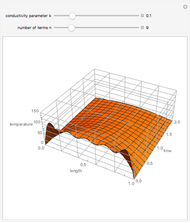
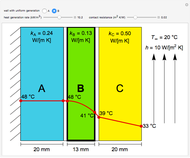
This Demonstration calculates temperature as a function of distance from the base of a fin of uniform cross-sectional area. The fin is attached to a base, which has the same cross-sectional area and is at a constant temperature of 100 °C. Heat loss from the fin is by natural convection to the surrounding air, which is at 25 °C. The rate of heat transfer is calculated for an adiabatic tip (no heat transfer through the tip surface) and for a tip that has heat transfer by convection. The temperature decreases down the fin due to conduction and to heat being lost by convection. The conduction is assumed to be one-dimensional along the length of the fin. Use sliders to vary the dimensions of the fin.
[more]
Contributed by: Benjamin L. Kee and Rachael L. Baumann (March 2014)
Additional contributions by: John L. Falconer
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The axial temperature distributions for a fin of uniform cross section for an adiabatic tip  and a tip with convection
and a tip with convection 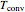 are:
are:
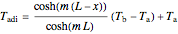 ,
,
 ,
,
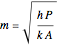 ,
,
for a rectangular fin:
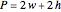 ,
,
 ,
,
for a pin fin:
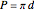 ,
,
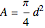 ,
,
where  and
and  are the base and ambient air temperatures,
are the base and ambient air temperatures, 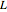 is fin length (m),
is fin length (m),  is position down the fin (m),
is position down the fin (m), 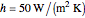 is the convection heat transfer coefficient,
is the convection heat transfer coefficient,  is the thermal conductivity of the material (W/(m K)),
is the thermal conductivity of the material (W/(m K)),  is a simplification term,
is a simplification term,  is fin perimeter (m),
is fin perimeter (m), 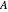 is the fin cross-sectional area (
is the fin cross-sectional area (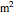 ),
), 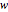 and
and  are the width and height of the rectangular fin (m) and
are the width and height of the rectangular fin (m) and  is the pin fin diameter (m).
is the pin fin diameter (m).
The fin heat transfer rates for each tip condition are:
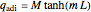 ,
,
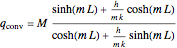 ,
,
 ,
,
where  is in W, and
is in W, and 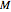 is a simplification term.
is a simplification term.
The thermal conductivities for the fin materials are:
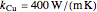 ,
,
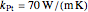 ,
,
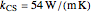 .
.
Reference
[1] T. L. Bergman, A. S. Lavine, F. P. Incropera and D. P. DeWitt, Introduction to Heat Transfer, 6th ed., Hoboken: John Wiley and Sons, 2011 p. 161.
Permanent Citation