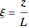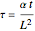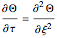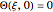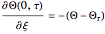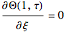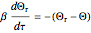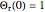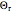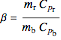Heat Transfer between a Bar and a Fluid Reservoir: A Coupled PDE-ODE Model
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
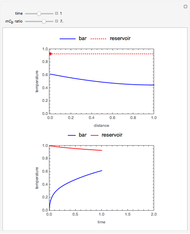
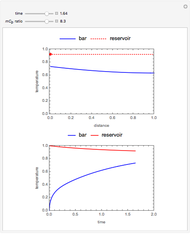
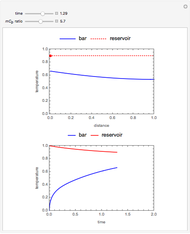
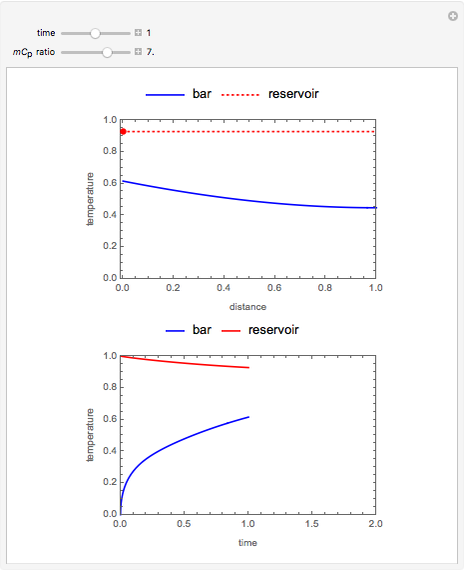
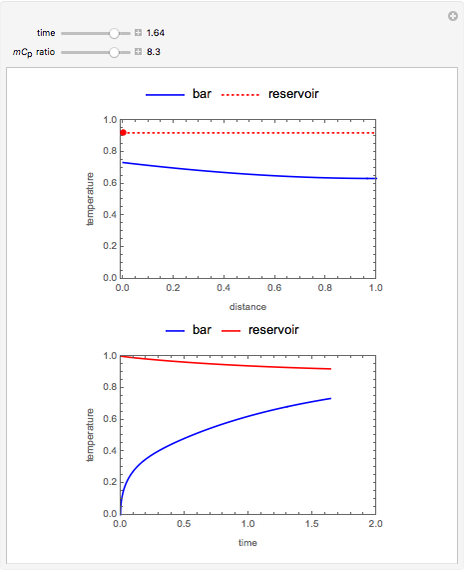
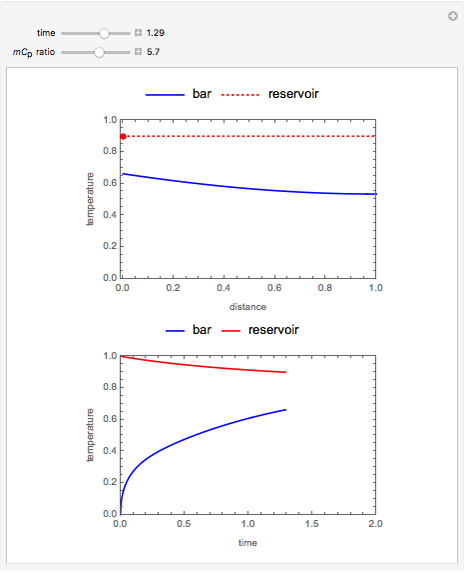
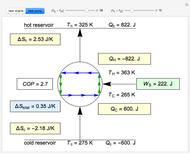
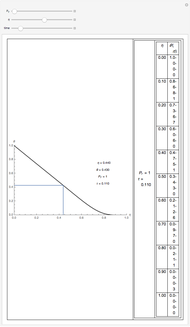
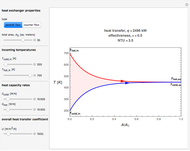
Consider a thin bar of length 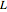 with initial temperature
with initial temperature 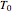 . The right end and the sides of the bar are insulated. For times
. The right end and the sides of the bar are insulated. For times 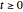 , the left end is connected to a well-mixed insulated reservoir at an initial temperature
, the left end is connected to a well-mixed insulated reservoir at an initial temperature 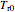 . This Demonstration determines the transient temperature of the bar and the reservoir.
. This Demonstration determines the transient temperature of the bar and the reservoir.
Contributed by: Clay Gruesbeck (September 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation