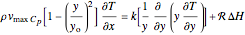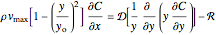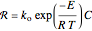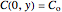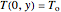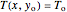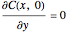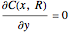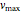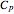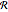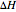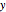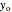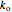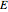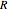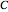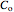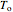Heat Transport and Chemical Reaction in Tubular Reactor with Laminar Flow

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
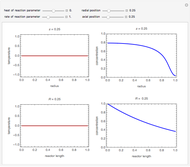
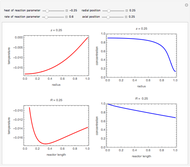
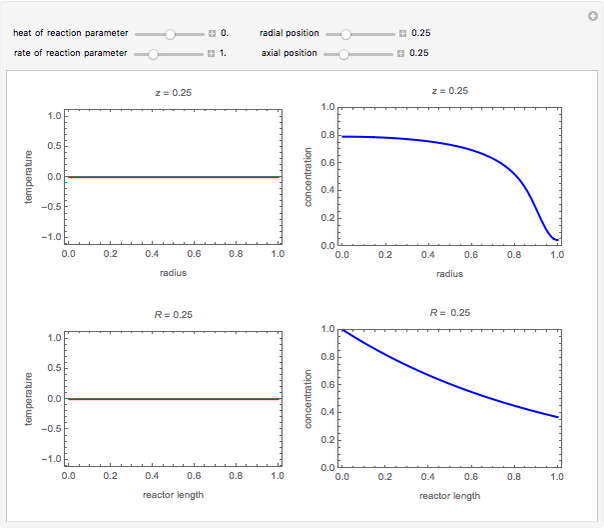
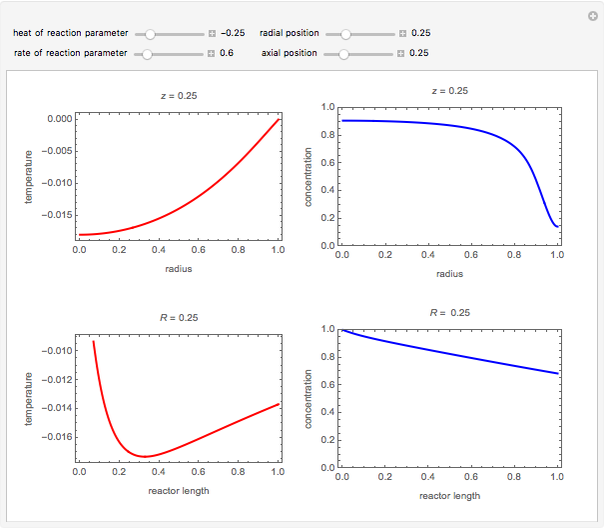
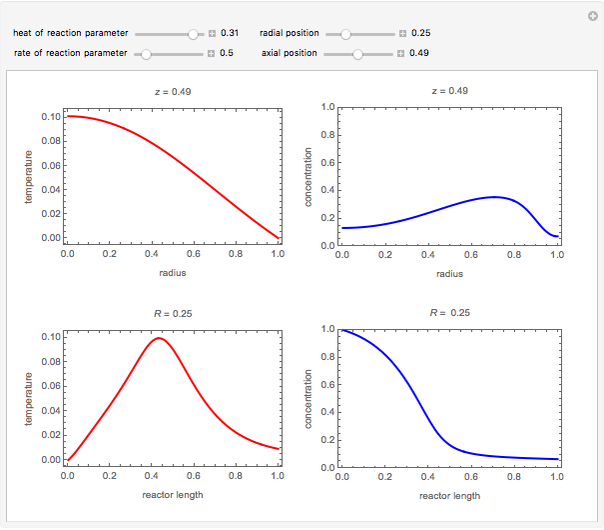
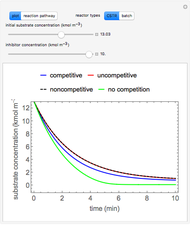
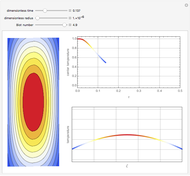
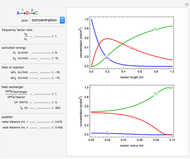
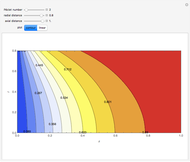
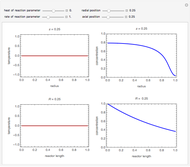
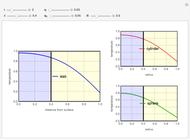
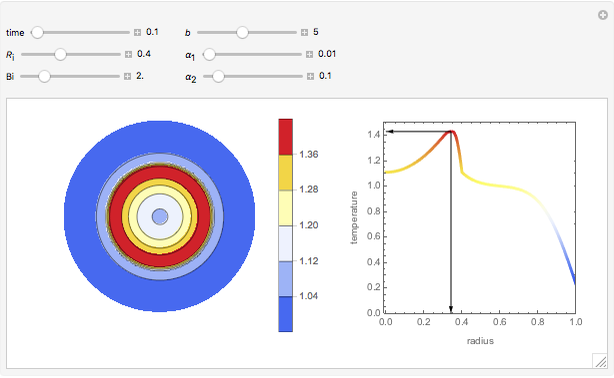
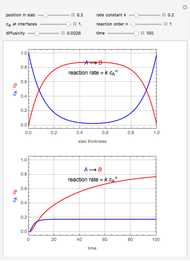
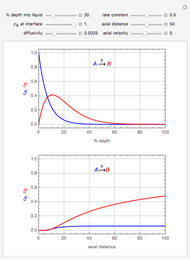
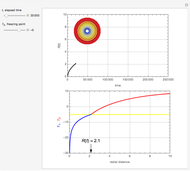
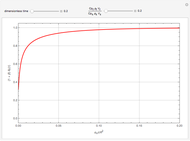
This Demonstration shows the temperature and concentration profiles of an insulated tubular reactor in which a first-order, irreversible reaction 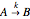 takes place in a fluid undergoing laminar flow.
takes place in a fluid undergoing laminar flow.
Contributed by: Clay Gruesbeck (April 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
It is convenient to use the following dimensionless quantities:
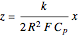 ,
,
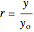 ,
,
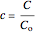 ,
,
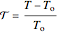 ;
;
here 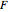 is the mass flow rate divided by the cross-sectional area of the tubular reactor.
is the mass flow rate divided by the cross-sectional area of the tubular reactor.
The dimensionless form of the conservation equations is:
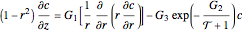 ,
,
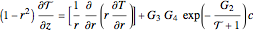 ,
,
with the boundary conditions:
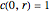 ,
,
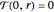 ,
,
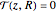 ,
,
 ,
,
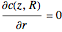 .
.
Dimensionless parameters are defined as follows:
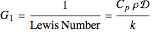 ,
,
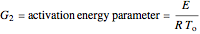 ,
,
 ,
,
 .
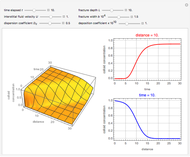
This system of coupled differential equations is solved with the built-in function NDSolve, and the radial and axial profiles of temperature and concentration of reactant
.
This system of coupled differential equations is solved with the built-in function NDSolve, and the radial and axial profiles of temperature and concentration of reactant 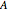 are shown for different values of the radial and axial distance, the rate of reaction parameter
are shown for different values of the radial and axial distance, the rate of reaction parameter 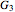 and the heat of reaction parameter
and the heat of reaction parameter 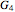 .
.
Reference
[1] R. I. Rothenberg and J. M. Smith, "Heat Transfer and Reaction in Laminar Tube Flow," AIChE Journal, 12 (2), 1966 pp. 213–220. doi:10.1002/aic.690120204.
Permanent Citation