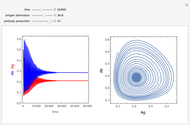
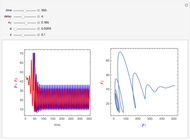
Hemodialysis

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
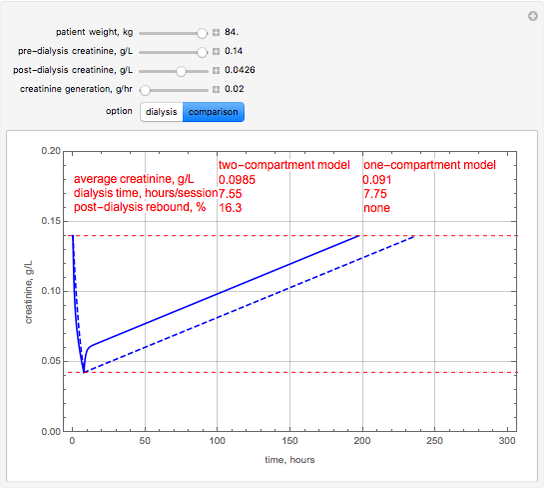
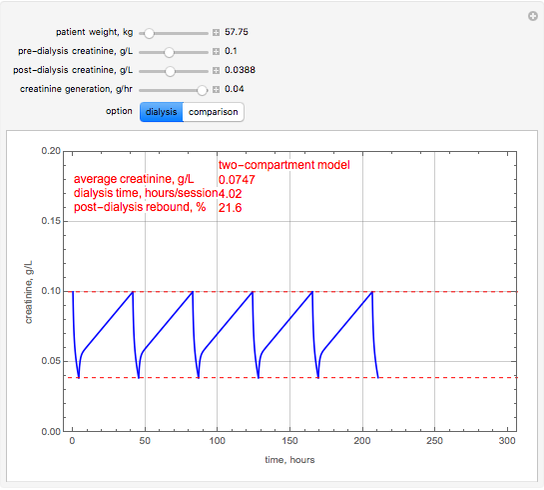
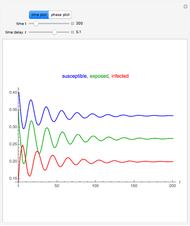
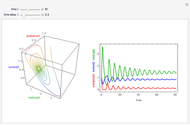
This Demonstration uses the pharmacokinetic one- and two-compartment models to simulate hemodialysis.
Contributed by: Clay Gruesbeck (July 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
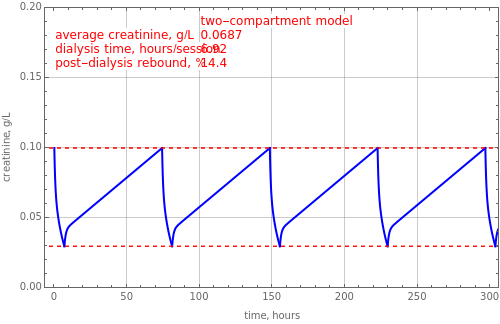
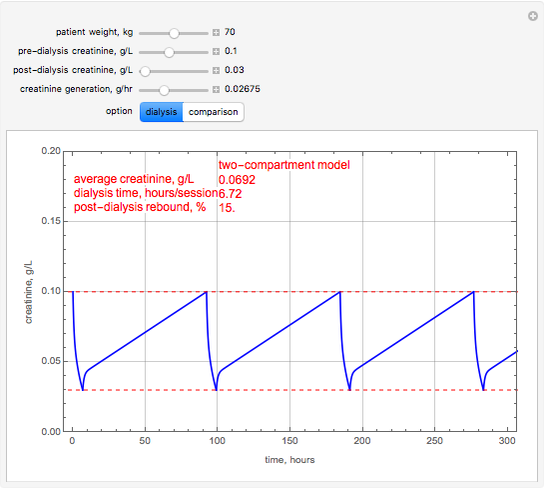
In the one-compartment model, the patient's body fluid is considered as one unit; toxins, here represented by creatinine, are removed to the dialyzer by diffusion. The two-compartment model assumes the body fluids are divided into two compartments, one directly accessible to the dialyzer (extracellular) and the other indirectly accessible (intracellular); creatinine is generated in the extracellular compartment [1]. Assuming constant volume and no residual kidney function, the one-compartment model is described by an ordinary differential equation:

and the two-compartment model by a pair of coupled ordinary differential equations:
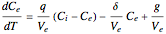
and
 .
.
Here 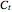 ,
,  , and
, and 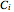 are the creatinine concentrations in the total, extracellular, and intracellular compartments;
are the creatinine concentrations in the total, extracellular, and intracellular compartments;  is the mass transfer coefficient;
is the mass transfer coefficient;  is the dialyzer clearance; and
is the dialyzer clearance; and  ,
,  , and
, and 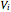
 are the total, extracellular, and intracellular volumes. Total body volume in liters is taken as 57% of body weight in kilograms, and the intracellular and extracellular volumes as 2/3 and 1/3 of total body volume [2].
are the total, extracellular, and intracellular volumes. Total body volume in liters is taken as 57% of body weight in kilograms, and the intracellular and extracellular volumes as 2/3 and 1/3 of total body volume [2].  is the rate of creatinine generation and
is the rate of creatinine generation and 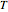 is time. The initial condition for the dialysis time period is
is time. The initial condition for the dialysis time period is  , a constant, in the recovery period (no dialysis)
, a constant, in the recovery period (no dialysis) 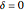 , and the initial values of
, and the initial values of 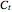 ,
,  , and
, and  are equal to the values of
are equal to the values of 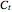 ,
,  , and
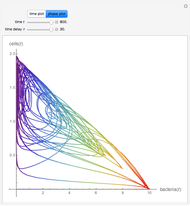
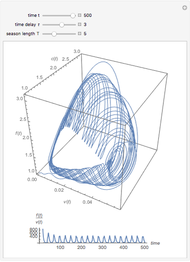
, and  at the end of dialysis. These equations are solved using Mathematica's built-in function NDSolve. The solution to the two-compartment model exhibits the phenomena of post-dialysis rebound, the observed fast increase in creatinine concentration after dialysis caused by disequilibrium between the compartments.
at the end of dialysis. These equations are solved using Mathematica's built-in function NDSolve. The solution to the two-compartment model exhibits the phenomena of post-dialysis rebound, the observed fast increase in creatinine concentration after dialysis caused by disequilibrium between the compartments.
References
[1] J. Waniewski, "Mathematical Modeling of Fluid and Solute Transport in Hemodialysis and Peritoneal Dialysis," Journal of Membrane Science, 274(1–2), 2006 pp. 24–37. doi:10.1016/j.memsci.2005.11.038.
[2] K. B. G. Sprenger, W. Kratz, A. E. Lewis, and U. Stadtmüller, "Kinetic Modeling of Hemodialysis, Hemofiltration, and Hemodiafiltration," Kidney International, 24, 1983 pp. 143–151. doi:10.1038/ki.1983.138.
Permanent Citation