Hexagrammum Mysticum

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
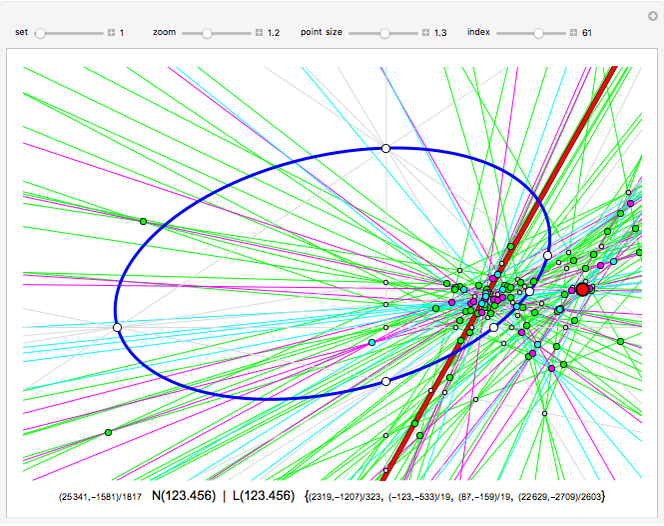
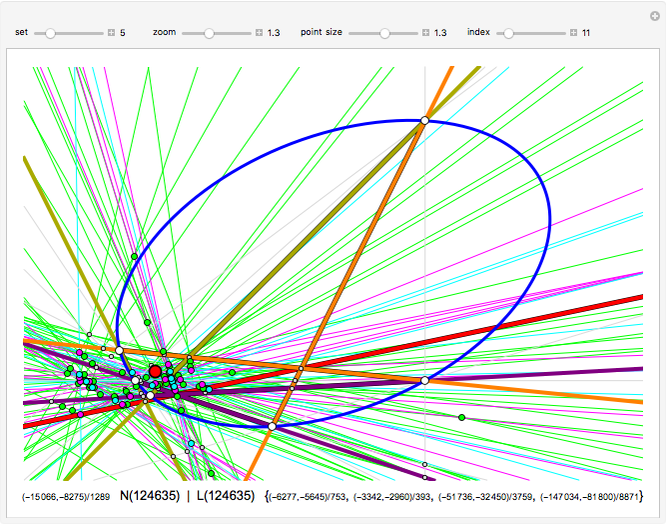
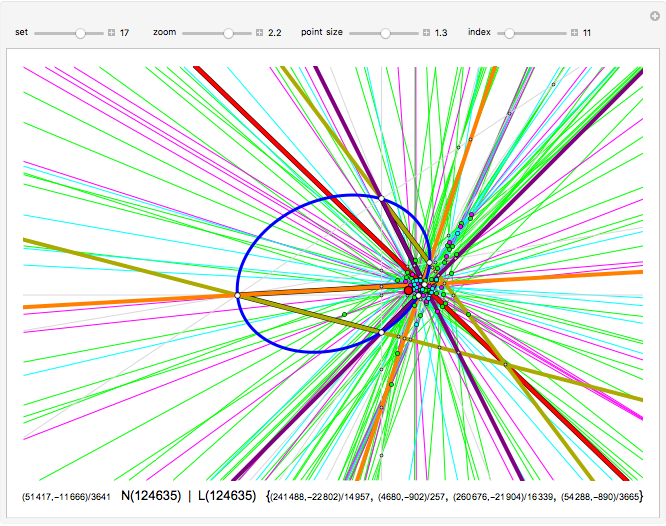
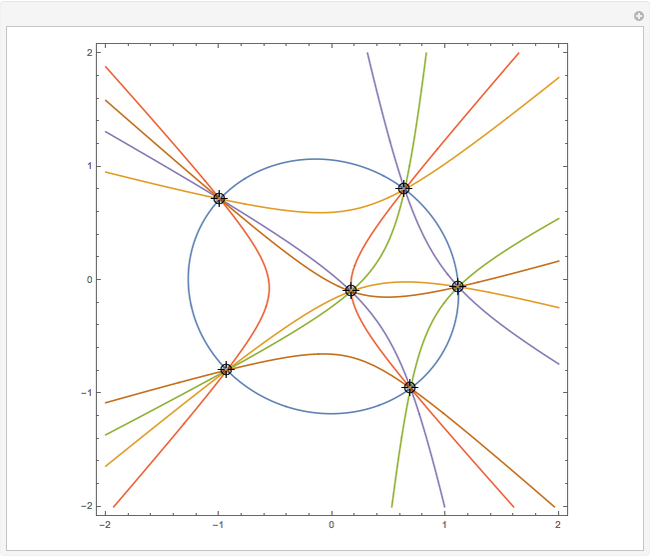
Consider six points on a conic section (circle, ellipse, parabola or hyperbola). Label them B L A I S E and connect them to form a hexagon. There are 15 ways to choose two points, leading to 15 lines that intersect at 45 points.
[more]
Contributed by: Ed Pegg Jr (August 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Points are sometimes called nodes, giving the N part of N(BLAISE), N(BAS.LIE) and N(BL.AI.SE) in the Kirkman, Steiner and Salmon points.
References
[1] Wikipedia. "Pascal's Theorem." (Aug 21, 2017) en.wikipedia.org/wiki/Pascal%27 s_theorem.
[2] Wikipedia. "Blaise Pascal." (Aug 21, 2017) en.wikipedia.org/wiki/Blaise_Pascal.
[3] Wikipedia. "Thomas Kirkman." (Aug 21, 2017) en.wikipedia.org/wiki/Thomas_Kirkman.
[4] Wikipedia. "Arthur Cayley." (Aug 21, 2017) en.wikipedia.org/wiki/Arthur_Cayley.
[5] Wikipedia. "Jakob Steiner." (Aug 21, 2017) en.wikipedia.org/wiki/Jakob_Steiner.
[6] Wikipedia. "Julius Plücker." (Aug 21, 2017) en.wikipedia.org/wiki/Julius_Pl%C3%BCcker.
[7] Wikipedia. "George Salmon." (Aug 21, 2017) en.wikipedia.org/wiki/George_Salmon.
[8] J. Conway and A. Ryba, "The Pascal Mysticum Demystified," The Mathematical Intelligencer, 34(3), 2012 pp. 4–8. doi:10.1007/s00283-012-9301-4.
Permanent Citation
"Hexagrammum Mysticum"
http://demonstrations.wolfram.com/HexagrammumMysticum/
Wolfram Demonstrations Project
Published: August 24 2017