Hidden Periodicity in Quality Control Records

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
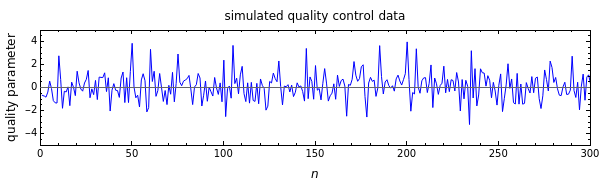
Many fluctuating industrial quality control charts appear as random time series but may be hiding an underlying periodicity. While such periodicity can be practically undetectable in the raw record, it is clearly revealed in an autocorrelation plot. This is shown with simulated random records having different periodicities.
Contributed by: Mark D. Normand and Micha Peleg (July 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
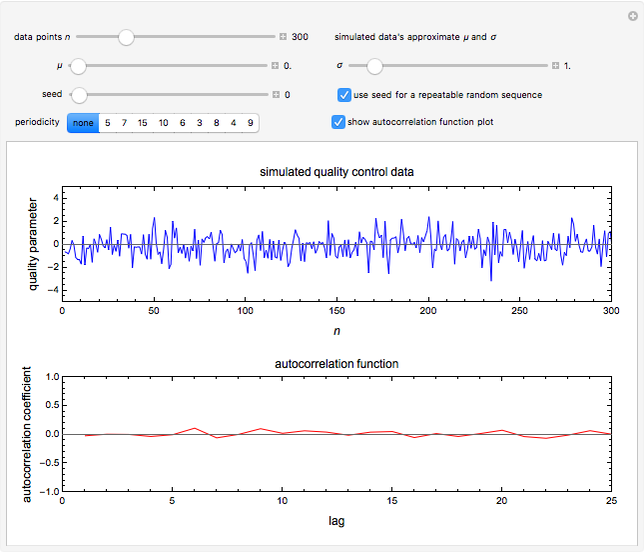
Snapshot 1: simulated quality control record with no hidden periodicity
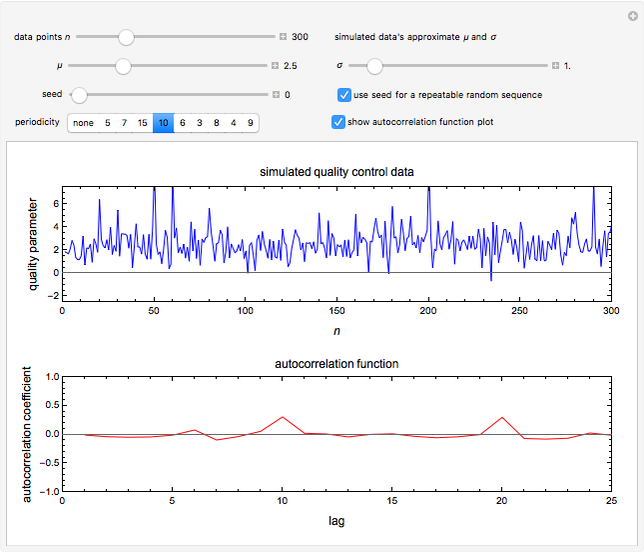
Snapshot 2: simulated quality control record with a hidden periodicity of 10
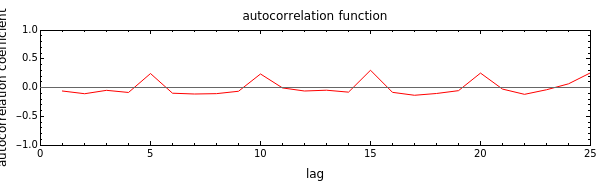
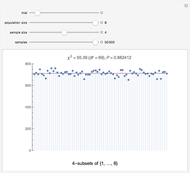
Snapshot 3: the simulated quality control record with a hidden periodicity of 10 with its autocorrelation function’s plot shown
Snapshot 4: simulated quality control record with a hidden periodicity of 3
Snapshot 5: the simulated quality control record with a hidden periodicity of 3 with its autocorrelation function’s plot shown
A typical industrial quality control chart is the displayed record of a measured quality parameter (physical, chemical, biological) plotted versus time. It frequently looks like a fluctuating random time series, and as long as the entries remain within an acceptable range, the process is considered stable and under control. Such a record, however, may have hidden periodicity, where the process might be particularly vulnerable to a mishap. Such periodicity is usually undetectable to casual visual inspection of the record itself but can be easily detected in the plot of its autocorrelation function (ACF).
This Demonstration simulates quality control charts by generating random time series having normal distribution. When a periodicity,  , is chosen by clicking a setter, the absolute value of every random
, is chosen by clicking a setter, the absolute value of every random 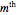 entry is enhanced by an arbitrary factor between 1.5 and 2.0, and the record is plotted. The record’s length
entry is enhanced by an arbitrary factor between 1.5 and 2.0, and the record is plotted. The record’s length  , the normal distribution’s mean
, the normal distribution’s mean  and standard deviation
and standard deviation  , and the random generation seed are all chosen with sliders.
, and the random generation seed are all chosen with sliders.
To display the autocorrelation function, click the "show autocorrelation function plot" checkbox. The periodicity of the particular setting appears as repeatable peaks. Altering the record’s length  , the distribution’s
, the distribution’s  or
or  , or the random seed can enhance or flatten the peaks marking the periodicity.
, or the random seed can enhance or flatten the peaks marking the periodicity.
References
[1] M. Peleg, M. D. Normand, and M. G. Corradini, "Translating Randomly Fluctuating QC Records into the Probabilities of Future Mishaps," Mathematical and Statistical Methods in Food Science and Technology (D. Granato and G. Ares, eds.), New York: John Wiley & Sons, 2013 pp. 471–490.
[2] P. H. Tsarouhas, "Application of Statistical Approaches for Analysing the Reliability and Maintainability of Food Production Lines: A Case Study of Mozzarella Cheese," Mathematical and Statistical Methods in Food Science and Technology (D. Granato and G. Ares, eds.), New York: John Wiley & Sons, 2014 pp. 491–510.
[3] M. Peleg, "Estimating the Probability of High Microbial Counts Using Excel," (Feb 18, 2013). people.umass.edu/aew2000/MicCountProb/microbecounts.html.
Permanent Citation