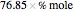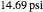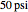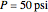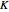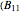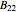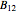High-Pressure Vapor-Liquid Equilibrium Computations Using the Hayden-O'Connell Method and Wilson Model

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
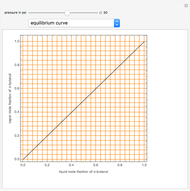
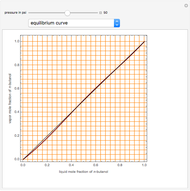
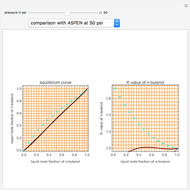
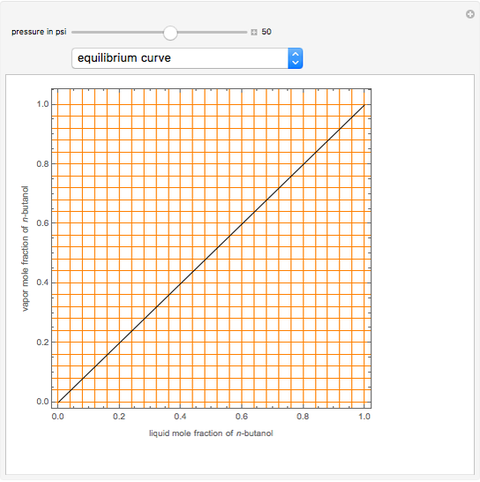
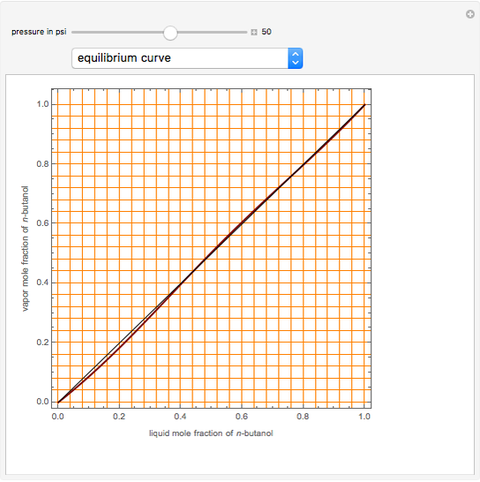
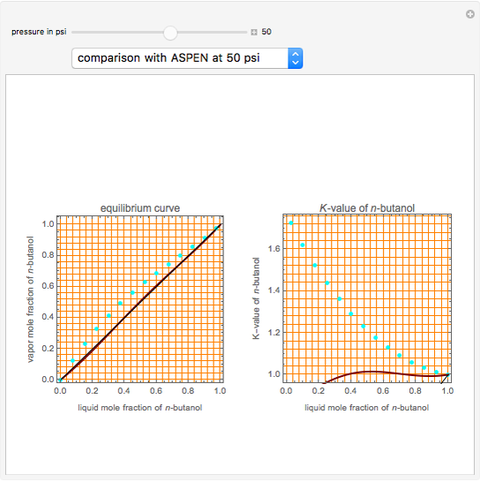
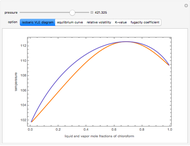
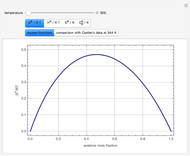
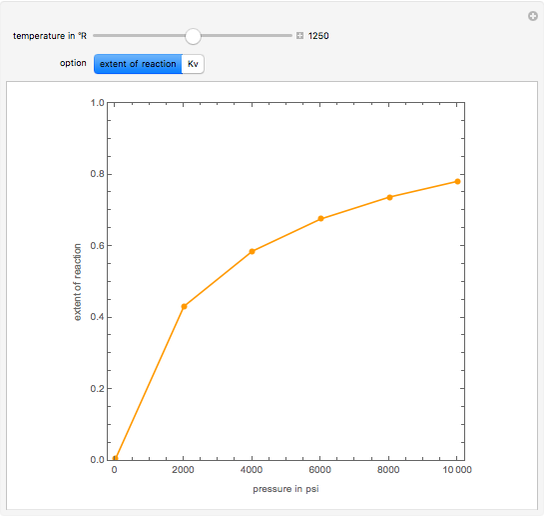
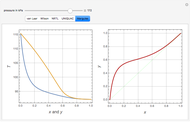
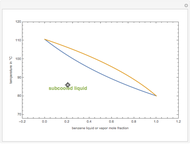
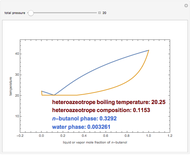
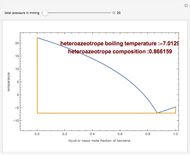
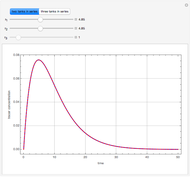
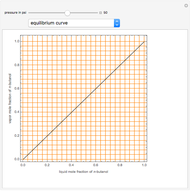
Consider a binary mixture of  -butanol and
-butanol and  -butyl acetate. This Demonstration computes vapor-liquid equilibrium data for this mixture at various pressures. We use the Wilson model for the prediction of liquid-phase activity coefficients and the Hayden–O'Connell method to compute the gas-phase fugacity coefficients.
-butyl acetate. This Demonstration computes vapor-liquid equilibrium data for this mixture at various pressures. We use the Wilson model for the prediction of liquid-phase activity coefficients and the Hayden–O'Connell method to compute the gas-phase fugacity coefficients.
Contributed by: Housam Binous and Eid Al-Mutairi (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] J. G. Hayden and J. P. O'Connell, "A Generalized Method for Predicting Second Virial Coefficients," Industrial and Engineering Chemistry Process Design and Development, 14(3), 1975, pp. 209–216.
Permanent Citation