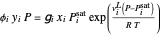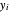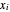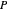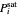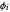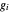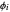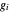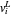High-Pressure Vapor-Liquid Equilibrium Data for a Binary Mixture: the Poynting Factor Correction

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Consider a binary mixture composed of 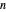 -hexane and
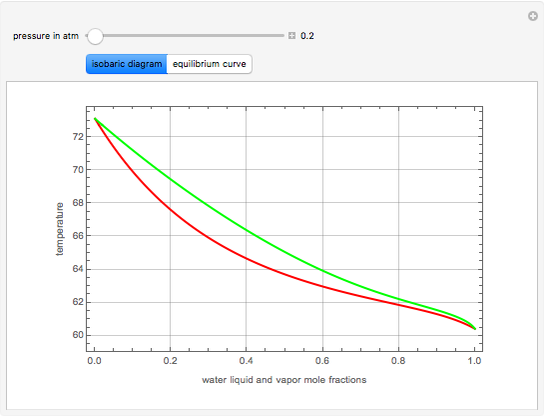
-hexane and 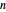 -heptane. This Demonstration computes and plots the isobaric vapor-liquid equilibrium diagram, the equilibrium curve, the relative volatility, the
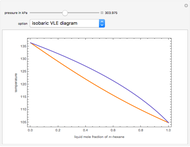
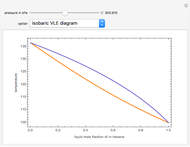
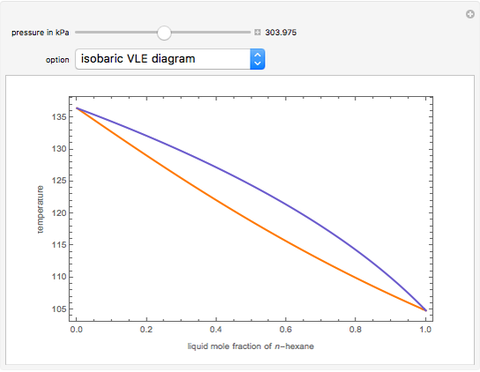
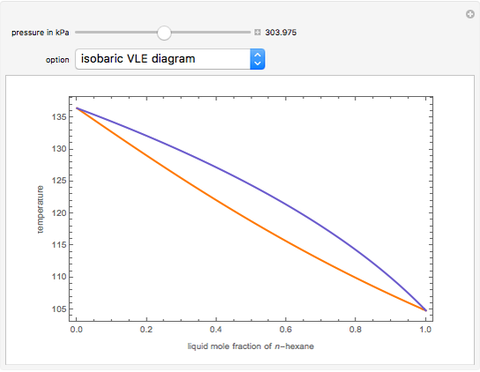
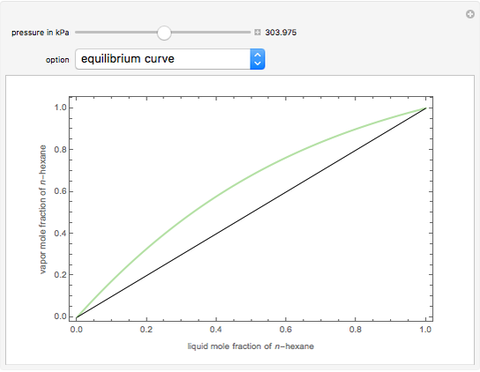
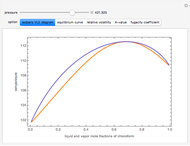
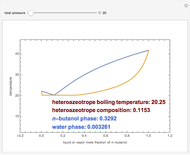
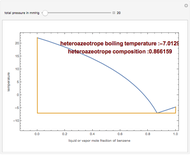
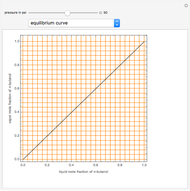
-heptane. This Demonstration computes and plots the isobaric vapor-liquid equilibrium diagram, the equilibrium curve, the relative volatility, the 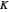 -value, the gas-phase fugacity coefficients using the Soave–Redlich–Kwong equation of state (EOS), and the Poynting correction factor for user-specified values of the pressure. The Demonstration takes into account deviation from ideal behavior in the gas phase by including gas phase fugacity coefficients. Thus high-pressure VLE data can be obtained. This Demonstration allows for the Poynting factor correction. Snapshots present calculations at a pressure approximately equal to 303.975 kPa.
-value, the gas-phase fugacity coefficients using the Soave–Redlich–Kwong equation of state (EOS), and the Poynting correction factor for user-specified values of the pressure. The Demonstration takes into account deviation from ideal behavior in the gas phase by including gas phase fugacity coefficients. Thus high-pressure VLE data can be obtained. This Demonstration allows for the Poynting factor correction. Snapshots present calculations at a pressure approximately equal to 303.975 kPa.
Contributed by: Housam Binous (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For more information about pressure effects, the Rackett equation, and the Pitzer–Curl method, see
[1] M. F. Doherty and M. F. Malone, Conceptual Design of Distillation Systems, New York: McGraw-Hill, 2001.
[2] B. E. Poling, J. M. Prausnitz, and J. P. O'Connell, The Properties of Gases and Liquids, 5th ed., New York: McGraw-Hill, 2004.
For more information about the SRK equation of state and the Wilson activity coefficients, see
[3] S. I. Sandler, Chemical and Engineering Thermodynamics, New York: John Wiley & Sons, 1999.
[4] J. R. Elliot and C. T. Lira, Introductory Chemical Engineering Thermodynamics, Upper Saddle River, NJ: Prentice Hall, 1999.
Permanent Citation