Hilbert Space Bases for Distinguishing Pure Quantum States in Low Dimensions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
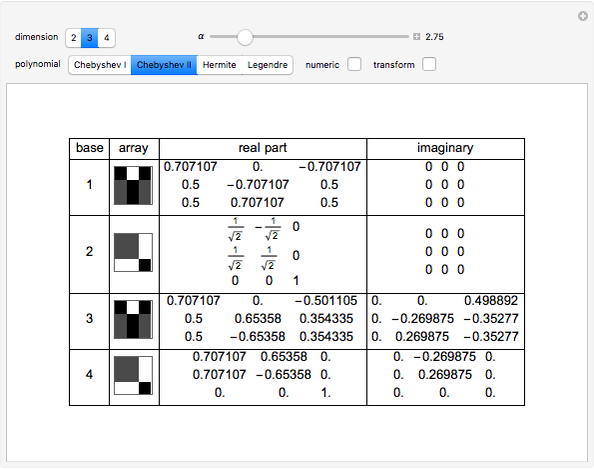
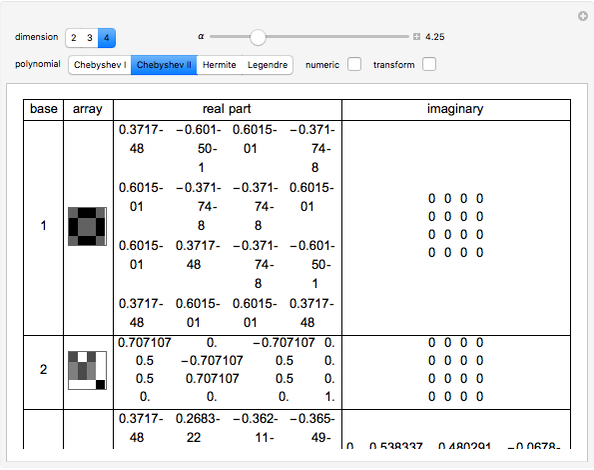
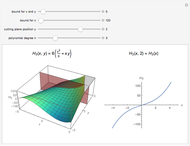
In a Hilbert space 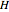 of arbitrary dimension, at least four orthonormal vector bases are needed to distinguish all pure quantum states. This Demonstration constructs the four bases using orthogonal polynomials (except for the case
of arbitrary dimension, at least four orthonormal vector bases are needed to distinguish all pure quantum states. This Demonstration constructs the four bases using orthogonal polynomials (except for the case 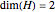 , in which only 3 are needed, and for
, in which only 3 are needed, and for 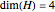 , for which the exact lower bound is an open problem). Since the one-dimensional case is trivial and five or more dimensions are hard to compute, the dimensions considered in this Demonstration are 2, 3 and 4. You can also adjust the complex phase parameter α used in the construction, choose an analytic or numeric calculation, choose a family of orthogonal polynomials with which the bases are constructed and transform the bases with a unitary matrix to make one of the bases canonical. Chebyshev I and Chebyshev II denote Chebyshev polynomials of the first and the second kind.
, for which the exact lower bound is an open problem). Since the one-dimensional case is trivial and five or more dimensions are hard to compute, the dimensions considered in this Demonstration are 2, 3 and 4. You can also adjust the complex phase parameter α used in the construction, choose an analytic or numeric calculation, choose a family of orthogonal polynomials with which the bases are constructed and transform the bases with a unitary matrix to make one of the bases canonical. Chebyshev I and Chebyshev II denote Chebyshev polynomials of the first and the second kind.
Contributed by: Wiljami Sillanpää (June 2017)
Suggested by: Teiko Heinosaari
Open content licensed under CC BY-NC-SA
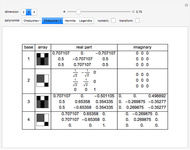
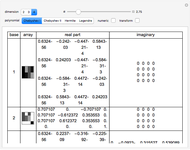
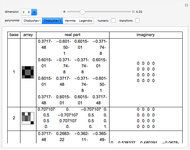
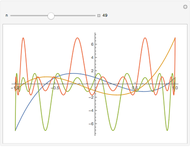
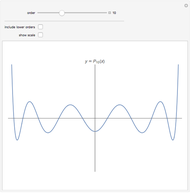
Snapshots
Details
Let 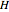 be a
be a  -dimensional Hilbert space with orthonormal bases
-dimensional Hilbert space with orthonormal bases  . Since the bases are of the form
. Since the bases are of the form  where
where 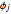 are the corresponding basis vectors, let
are the corresponding basis vectors, let  denote the projection on the
denote the projection on the 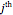 vector of the basis
vector of the basis 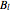 . Using this notation, the bases
. Using this notation, the bases  cannot distinguish pure states;
cannot distinguish pure states; 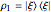 and
and 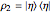 if and only if
if and only if 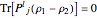 . It is shown in chapter 5 of [1] that for a system of four special bases, this condition implies
. It is shown in chapter 5 of [1] that for a system of four special bases, this condition implies 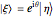 —that is, the states
—that is, the states 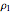 and
and 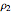 are essentially the same state. Thus, four bases can distinguish all pure states in any finite-dimensional Hilbert space. It is also proven in [1] that if
are essentially the same state. Thus, four bases can distinguish all pure states in any finite-dimensional Hilbert space. It is also proven in [1] that if  , only three orthonormal bases are needed.
, only three orthonormal bases are needed.
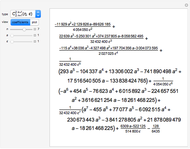
The four bases are constructed in the following way:
Let 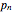 denote an orthogonal polynomial of order
denote an orthogonal polynomial of order  . For basis 1, the basis vectors are
. For basis 1, the basis vectors are 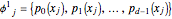 where
where  denotes the roots of
denotes the roots of  . Basis 2 is similar, except the
. Basis 2 is similar, except the  are now the roots of
are now the roots of 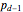 and the last basis vector is
and the last basis vector is 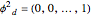 . Bases 3 and 4 are obtained from 1 and 2 simply by transforming each
. Bases 3 and 4 are obtained from 1 and 2 simply by transforming each 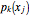 into
into  , where
, where 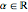 is not a rational multiple of
is not a rational multiple of  . All four bases can then be easily normalized. It is also important to note here that all of the bases are constructed using the same family of orthogonal polynomials. Curiously, when
. All four bases can then be easily normalized. It is also important to note here that all of the bases are constructed using the same family of orthogonal polynomials. Curiously, when  , bases 2 and 4 become identical. This method of construction is based on a paper by Jaming [2] and is also discussed in chapter 5 of [1].
, bases 2 and 4 become identical. This method of construction is based on a paper by Jaming [2] and is also discussed in chapter 5 of [1].
References
[1] C. Carmeli, T. Heinosaari, J. Schultz and A. Toigo, "How Many Orthonormal Bases are Needed to Distinguish All Pure Quantum States?," The European Physical Journal D, 69(179), 2015. doi:10.1140/epjd/e2015-60230-5.
[2] P. Jaming, "Uniqueness Results in an Extension of Pauli's Phase Retrieval Problem," Applied and Computational Harmonic Analysis, 37(3), 2014 pp. 413–441. doi:10.1016/j.acha.2014.01.003.
Permanent Citation