Hole-Free Magic 45-Ominoes

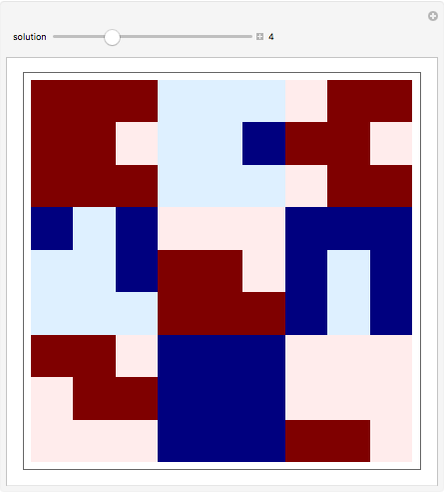
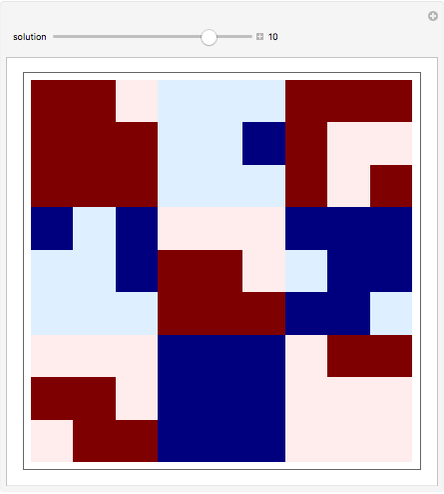
It is possible to construct connected configurations of cells (i.e. polyominoes) in a 9×9 square where each row, column, and main diagonal contains five cells within the configuration and each 3×3 block contains a number of squares corresponding to a number in the magic square containing all the digits between 1 and 9. Only 12 of the solutions to this problem are free of holes, where a hole is a set of cells outside the polyomino disconnected from the outside of the 9×9 square.