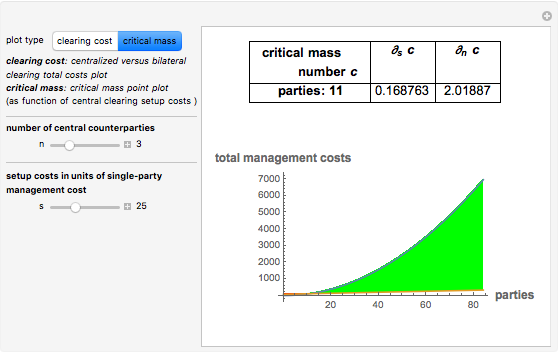
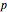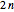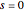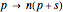"The more people participate in a system, the more it makes sense for a central authority to mediate their relationships/communication; no matter what the cost for setting up this central authority, as the number of participants increases, this cost is dwarfed by the benefits of centralized mediation on a linear versus quadratic basis".
This concept is applied here to make the argument that financial trading institutions should welcome centralized clearing of all derivatives trades.
The variable  is the number of central counterparties. Ideally
is the number of central counterparties. Ideally  would be equal to 1. Allowing
would be equal to 1. Allowing  to vary takes into account the idea that in practice it would be hard to implement a single clearing party for all trades. For example, the central authority of a currency would oppose releasing that authority to an international entity. Furthermore, the central clearing unit may lack the power to assess credit risks on a wide variety of trades in a timely fashion. The proposal is to have a hierarchical interconnected structure where information on assets and liabilities for each party is aggregated and passed on to the next layer, which is then propagated higher to the other clearing entities. This maintains the information transparency that helps eliminate duplicate margin requirements.
to vary takes into account the idea that in practice it would be hard to implement a single clearing party for all trades. For example, the central authority of a currency would oppose releasing that authority to an international entity. Furthermore, the central clearing unit may lack the power to assess credit risks on a wide variety of trades in a timely fashion. The proposal is to have a hierarchical interconnected structure where information on assets and liabilities for each party is aggregated and passed on to the next layer, which is then propagated higher to the other clearing entities. This maintains the information transparency that helps eliminate duplicate margin requirements.
The plot shows that for  much smaller than the total number of participants
much smaller than the total number of participants 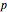 , (
, ( ), the benefit is still "linear versus quadratic". The variable
), the benefit is still "linear versus quadratic". The variable  is the setup cost for the central party in units of single-party management costs.
is the setup cost for the central party in units of single-party management costs.
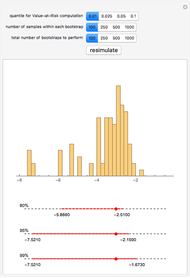
You can choose to plot the bilateral versus central counterparty costs by number of parties and see where it starts to make economic sense to have a central clearing party. Alternatively, you can see the plot for critical mass numbers of counterparty analysis, which is represented by three plots, for  ,
, 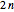 , or
, or  central counterparties.
central counterparties.
In addition, the table at the top shows the rounded critical mass number of parties as you select the various scenarios as well as the sensitivities of the unrounded critical mass number  with respect to
with respect to  or
or  .
.
By default  and
and 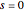 , i.e., there is only one single counterparty of reference and no extra cost to set up that central counterparty. This is the case discussed in the related web article cited in the references.
, i.e., there is only one single counterparty of reference and no extra cost to set up that central counterparty. This is the case discussed in the related web article cited in the references.  varies between 0 and 25
varies between 0 and 25 . Hence, the cursor for
. Hence, the cursor for  tends to move with
tends to move with  .
.
In the critical mass plot, the cost structure for the no central counterparty system is the quadratic plot function  . The cost structure for the
. The cost structure for the  central counterparties system is the linear plot
central counterparties system is the linear plot 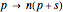 .
.
[less]