Hopf Bifurcation in a Biased van der Pol Oscillator

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
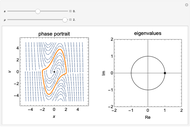
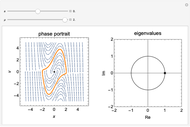
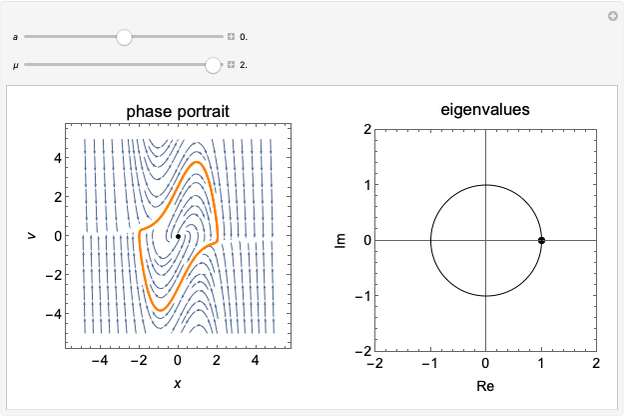
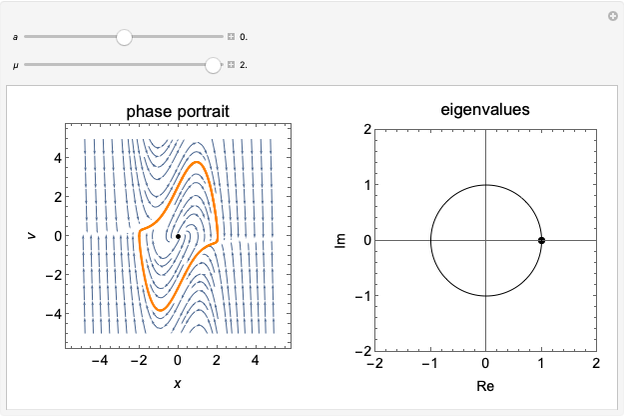
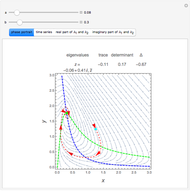
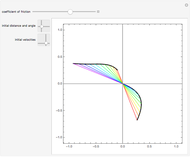
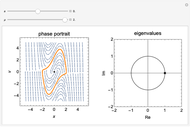
The biased van der Pol oscillator is represented by the nonlinear differential equation  (see Exercise 8.2.1 of [1]). This system is capable of exhibiting Hopf bifurcations, in which limit cycle attractors or repellers are created. Hopf bifurcations occur when eigenvalues for the fixed point cross the imaginary axis. When
(see Exercise 8.2.1 of [1]). This system is capable of exhibiting Hopf bifurcations, in which limit cycle attractors or repellers are created. Hopf bifurcations occur when eigenvalues for the fixed point cross the imaginary axis. When  , supercritical Hopf bifurcations occur at
, supercritical Hopf bifurcations occur at  or
or 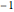 , and a stable limit cycle (attractor) is formed for
, and a stable limit cycle (attractor) is formed for 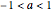 in the phase portrait. When
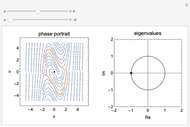
in the phase portrait. When 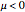 , a subcritical Hopf bifurcation occurs at
, a subcritical Hopf bifurcation occurs at  or
or 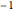 , and an unstable limit cycle (repeller) is found for
, and an unstable limit cycle (repeller) is found for 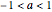 in the phase portrait. For
in the phase portrait. For  , a degenerate Hopf bifurcation occurs, in which there are an infinite number of periodic solutions but no limit cycles. No limit cycle is found outside the range
, a degenerate Hopf bifurcation occurs, in which there are an infinite number of periodic solutions but no limit cycles. No limit cycle is found outside the range 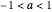 . In the phase portrait, an attractor is represented as a solid line and a repeller is represented as a dotted line.
. In the phase portrait, an attractor is represented as a solid line and a repeller is represented as a dotted line.
Contributed by: Tushar Mollik and Edmon Perkins (October 2018)
After work by: Steven H. Strogatz
Open content licensed under CC BY-NC-SA
Details
Reference
[1] S. H. Strogatz, Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering, 2nd ed., Boulder, CO: Westview, 2015.
Snapshots
Permanent Citation