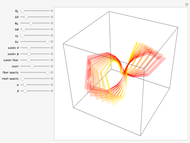
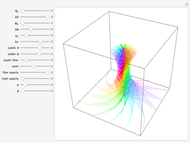
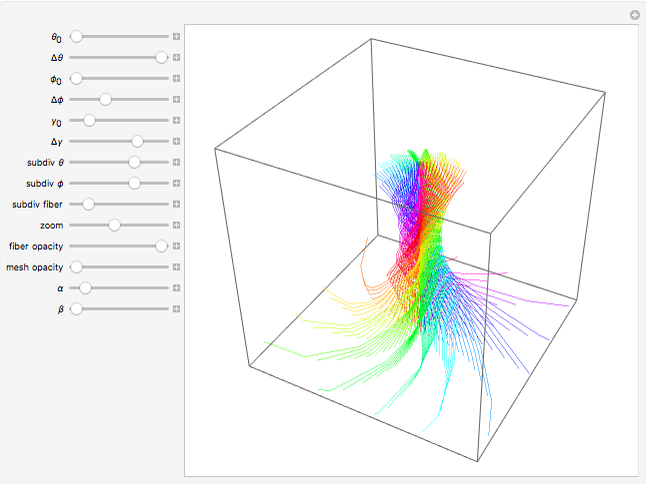
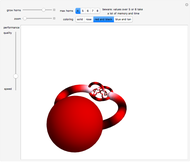
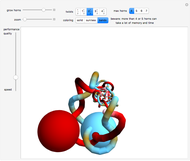
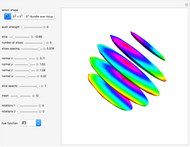
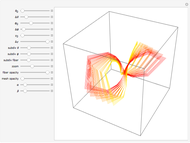
The Hopf fibration is a fibration of into fibers diffeomorphic to ; the quotient space is . In other words, the sphere can be used to parametrize the fibers of the Hopf fibration. is projected into via stereographic projection and each fiber intersects the top half of the unit sphere only once except for the equatorial fiber that intersects the upper unit hemisphere exactly along the equator; note that a hemisphere with its boundary identified to a point is diffeomorphic to .