Hyperbolic Triangle

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
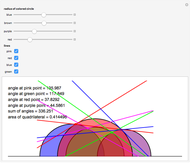
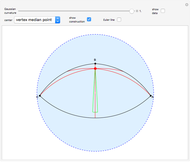
Using three semicircles, this Demonstration creates a hyperbolic triangle, measures and totals its angles, and calculates its area using the Gauss–Bonnet formula. You can vary the radii of the circles, thus changing all the measurements.
Contributed by: Michael Rach and Ron Grosz (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In the upper half-plane model of hyperbolic geometry, the hyperbolic straight lines are the vertical rays and the semicircles touching the  axis.
axis.
The measure of the angle formed by the intersection of two semicircles is calculated by measuring the angle of the tangents to the circles at that point. The angle sum of a hyperbolic triangle is less than 180 degrees.
The Gauss–Bonnet formula states that the area of a hyperbolic triangle is the difference of  (or 180°) and the sum of the interior angles of the triangle.
(or 180°) and the sum of the interior angles of the triangle.
References
C. Walkden, "The Gauss-Bonnet Theorem," lecture notes, Feb. 13, 2009.
A. G. Bennett, "Triangles, Angles, and Area," Active Learning and the World Wide Web, 1998.
S. Weintraub, "Tiling the Poincaré Disk," American Mathematical Society Feature Column, Feb. 1998.
R. E. Schwartz, "Ideal Triangle Groups, Dented Tori, and Numerical Analysis," Annals of Mathematics, 153, 2001 pp. 533–598.
Permanent Citation