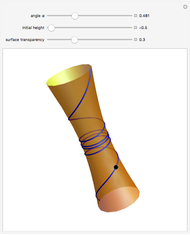
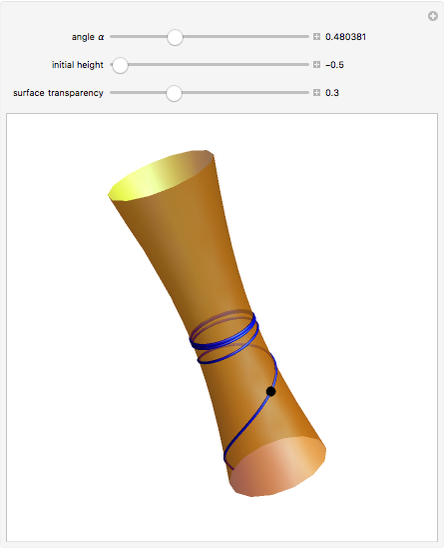
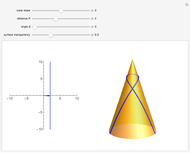
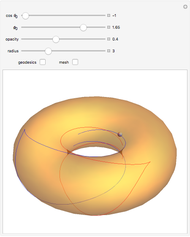
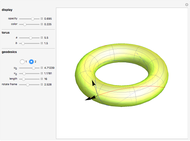
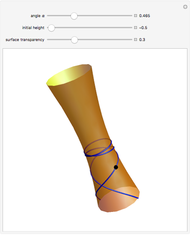
The image shows a one-sheeted hyperboloid symmetric around the axis. The blue curve is the unique hyperboloid geodesic passing through the given point (shown in black) and intersecting the parallel (i.e. the circle of latitude) through that point at the given angle . When is small enough, the geodesic stays in the lower half of the hyperboloid. When is equal to a certain critical value, the geodesic approaches the circle (i.e. the parallel with the smallest radius) but never reaches it. This critical value is stored as a bookmark (click the "+" button in the upper-right corner). For still higher values of , the geodesic crosses the circle and proceeds to the upper half of the hyperboloid.