Impact of Sample Size on Approximating the Triangular Distribution
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
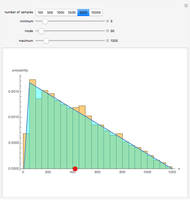
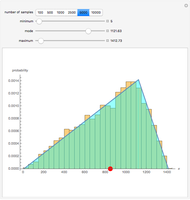
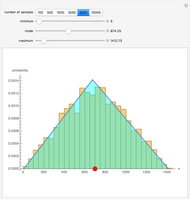
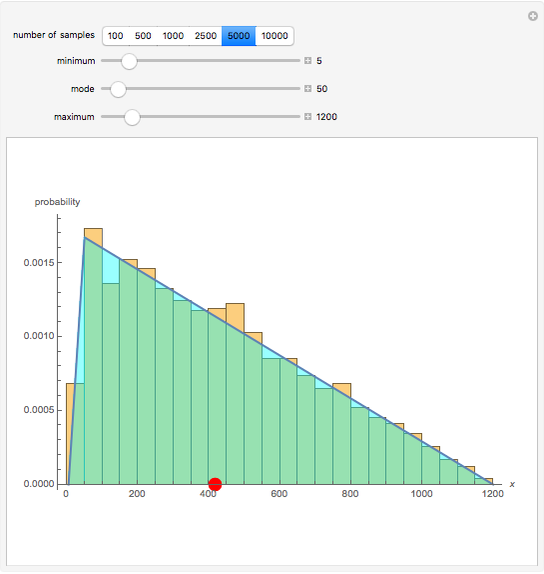
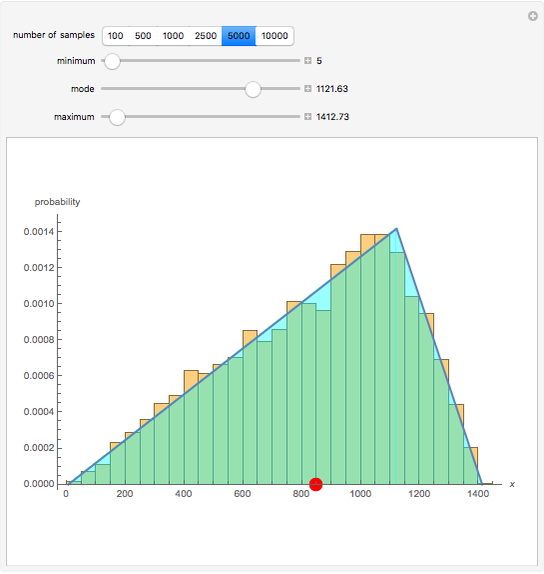
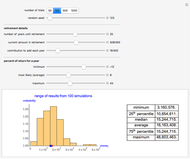
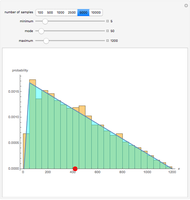
You can select the minimum, mode, and maximum parameter values for the triangular distribution. By definition, the minimum < mode < maximum. The sample probability distribution is compared to the theoretical distribution as you increase the sample size. In general, as the sample size increases, the more closely the sample distribution matches the theoretical distribution. The red dot shows the mean value for the theoretical distribution.
Contributed by: Paul Savory (University of Nebraska-Lincoln) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The triangular distribution is used in discrete-event and Monte Carlo simulation as a key probability distribution for modeling randomness. This Demonstration compares the sample triangular probability distribution with the theoretical distribution. Probability and statistical theory shows us that as the number of samples increases for the given parameter values, the more closely the sample probability distribution will resemble the theoretical distribution. You can verify this by specifying the minimum, mode, and maximum parameter values that describe a sample triangular probability distribution. The specified number of samples is randomly generated and compared to the theoretical distribution.
Impact of Sample Size on Approximating the Normal Distribution
Paul Savory (University of Nebraska-Lincoln)
Sampling Distribution of the Mean and Standard Deviation in Various Populations
Ian McLeod
Impact of Sample Size on Approximating the Uniform Distribution
Paul Savory (University of Nebraska-Lincoln)
Comparing Some Residuals for Generalized Linear Models
Darren Glosemeyer
Binomial Probability Distribution
Paul Savory (University of Nebraska ? Lincoln)
Estimating and Diagnostic Checking in Censored Normal Random Samples
Nagham Muslim Mohammad and Ian McLeod
Comparing Exact and Approximate Censored Normal Likelihoods
Ian McLeod and Nagham Muslim Mohammad
The Empirical Rule for Normal Distributions
Marc Brodie
Sample versus Theoretical Distribution
Joe Bolte
Calculating Sample Size
Daniel de Souza Carvalho
-
Monte Carlo Simulation of Retirement Savings with Variable Annual Return
Paul Savory -
Law of Large Numbers: Dice Rolling Example
Paul Savory -
Monte Carlo Simulation of Markov Prisoner
Paul Savory -
Law of Large Numbers: Comparing Relative versus Absolute Frequency of Coin Flips
Paul Savory -
Impact of Sample Size on Approximating the Uniform Distribution
Paul Savory -
Impact of Sample Size on Approximating the Triangular Distribution
Paul Savory -
Poor Statistical Qualities for the RANDU Random Number Generator
Paul Savory -
Impact of Sample Size on Approximating the Normal Distribution
Paul Savory -
Binomial Probability Distribution
Paul Savory -
Expected Number in Queue and System for an M/M/S Queue
Paul Savory -
Expected Time in System for M/G/1 Queue
Paul Savory -
Probability of Zero in a System for an M/M/S Queue
Paul Savory