Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Impedance of a Micro-Disk Microelectrode

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

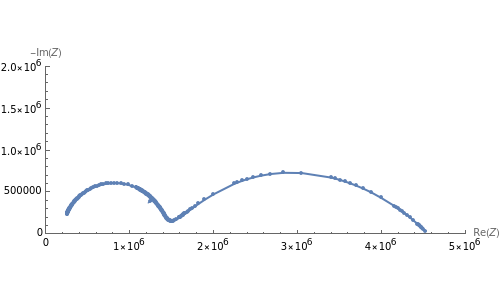
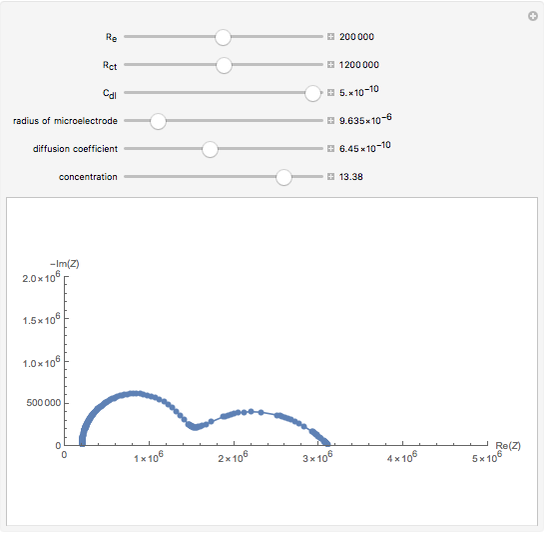
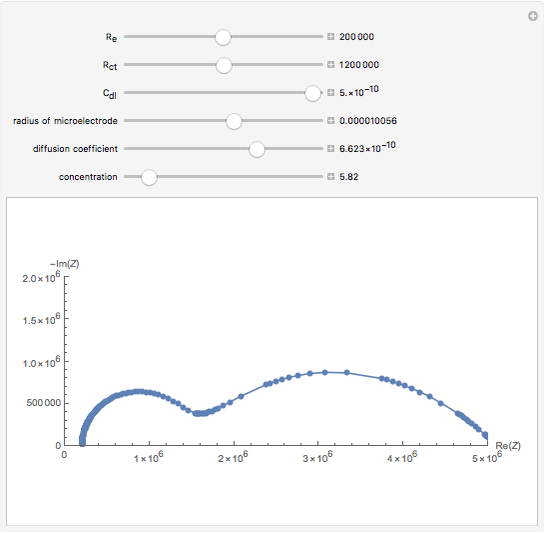
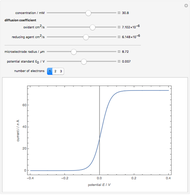
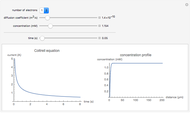
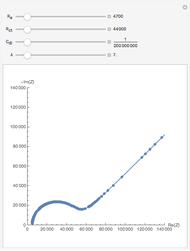
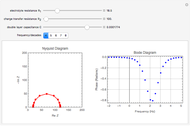
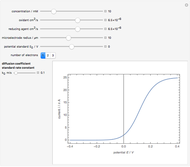
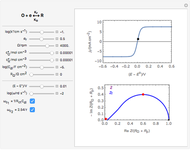
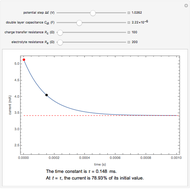
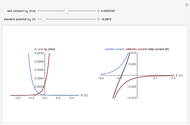
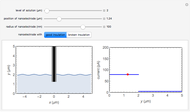
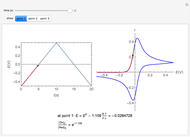
For the macroelectrode, one can use the Warburg impedance to describe the diffusion coefficient. This Demonstration shows the analytical solution for the diffusional impedance of a micro-disk electrode. It is a function of frequency, kinetics, concentration, and the radius of the microelectrode.

Contributed by: Quang-Dao Trinh (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send