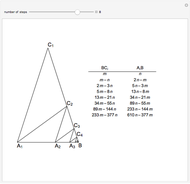
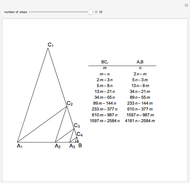
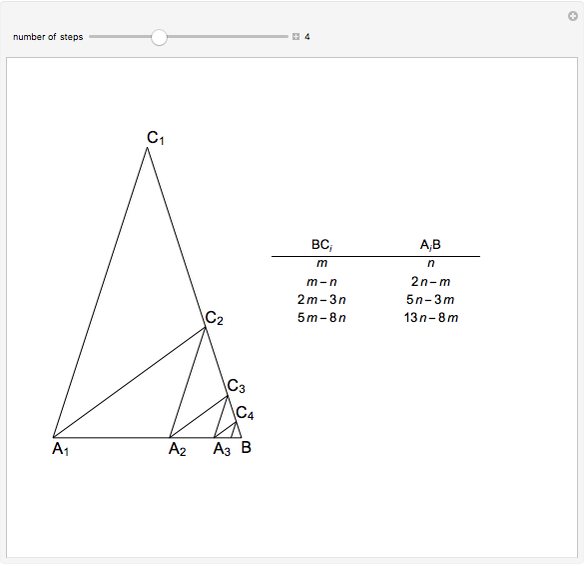
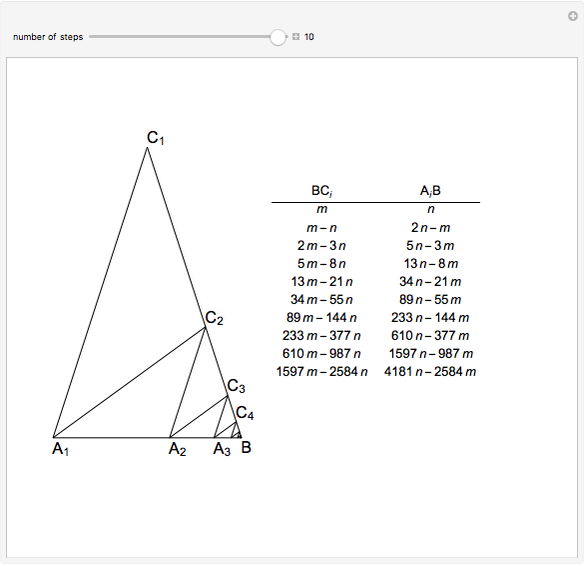
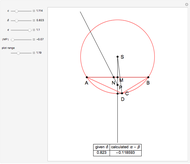
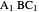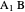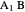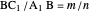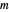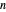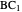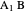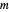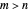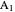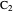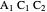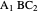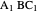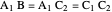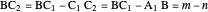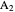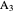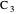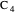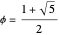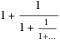In an isosceles triangle, if the measure of the leg angle is 72°, then the base and a leg are incommensurable. (Two lengths 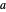 and
and  are called incommensurable if their ratio is irrational.)
are called incommensurable if their ratio is irrational.)
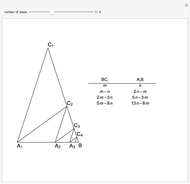
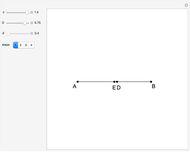
Let the vertices of the triangle be 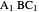 , where
, where 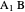 is the base. The angles are 72°, 72°, and 36°.
is the base. The angles are 72°, 72°, and 36°.
Assume that the ratio of  to
to 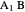 is rational, say
is rational, say 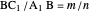 for positive integers
for positive integers 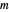 and
and 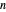 . For some appropriate unit of measurement, we can take the lengths of
. For some appropriate unit of measurement, we can take the lengths of 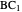 and
and 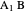 to be
to be 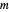 and
and  , where
, where 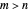 .
.
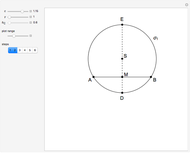
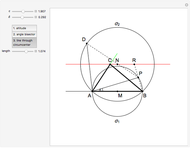
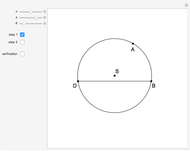
Bisect the angle at 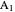 to meet the opposite side at
to meet the opposite side at 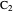 . The triangle
. The triangle 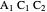 is an isosceles triangle because the angles are 36°, 36°, and 108°. The triangle
is an isosceles triangle because the angles are 36°, 36°, and 108°. The triangle  is an isosceles triangle because its angles are 72°, 72°, and 36° (
is an isosceles triangle because its angles are 72°, 72°, and 36° (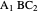 is similar to the original triangle
is similar to the original triangle 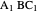 ). Therefore,
). Therefore, 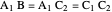 and
and 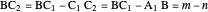 .
.
Iterating this construction gives the points 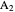 ,
, 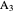 , … and
, … and 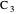 ,
, 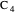 , … with
, … with  ,
,  , …, where each of the integers is positive and forms a strictly decreasing sequence, which is impossible.
, …, where each of the integers is positive and forms a strictly decreasing sequence, which is impossible.
Therefore, the ratio of the sides is irrational.
In fact, the ratio is 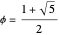 , the golden ratio. Its continued fraction is
, the golden ratio. Its continued fraction is 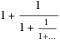 with cumulants 1, 2, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21, …; you can see the numerators and denominators in the table.
with cumulants 1, 2, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21, …; you can see the numerators and denominators in the table.
[less]

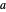 and
and  are called incommensurable if their ratio is irrational.)
are called incommensurable if their ratio is irrational.)