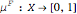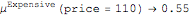Inference with Fuzzy IF-THEN Rules

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
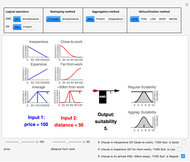
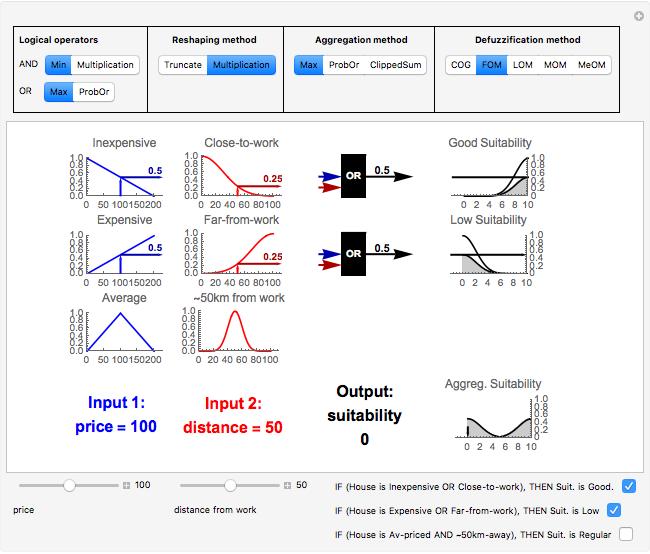
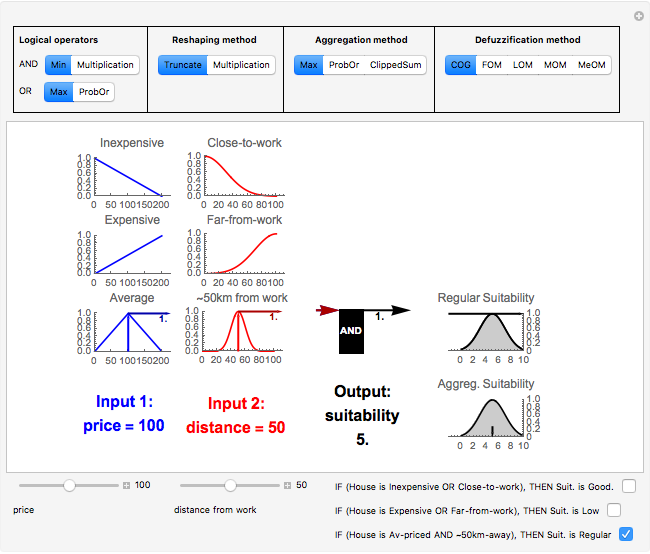
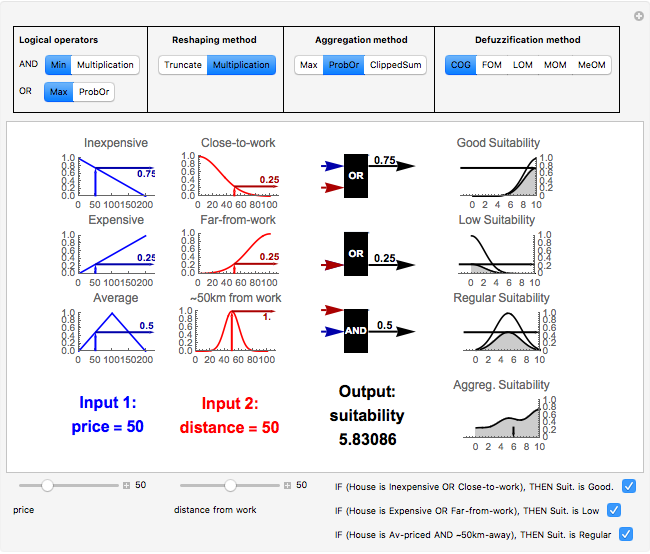
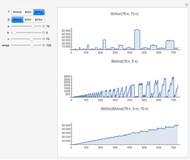
This Demonstration illustrates the interpolation method for a system of fuzzy IF-THEN rules. In particular, it shows how to calculate the suitability of a house given the following three rules: - IF (House is Inexpensive OR Close-to-work), THEN Suitability is Good. - IF (House is Expensive OR Far-from-work), THEN Suitability is Low. - IF (House is Average-priced AND About-50-km-from-work), THEN Suitability is Regular.
[more]
Contributed by: Luis R. Izquierdo and Segismundo S. Izquierdo (February 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration illustrates the so-called interpolation method for multiconditional approximate reasoning systems of fuzzy IF-THEN rules [1], including fuzzification and defuzzification. A particular instance of this method is Mamdani inference (also called max-min inference), which is often used in fuzzy control. Another particular instance is max-prod inference. The method consists of the following four steps:
1. Calculate the degree of consistency between the inputs and the antecedent of each IF-THEN rule. The Demonstration lets you choose different functions for the logical operators (AND, OR). As an example, consider the first rule at the top row, with antecedent "Inexpensive OR Close-to-work". The computation for crisp inputs price=110 and distance=57, using the function Max (maximum) as logical OR, would be: OR(Inexpensive(110), Close-to-work(57)) ⟶ OR(0.45,0.16) ⟶ Max(0.45,0.16) ⟶ 0.45. The result of this step is a number for each rule (i.e. the degree of consistency between the inputs and each rule's antecedent).
2. Reshape the original consequent of each rule (which is a fuzzy set), given the degree of consistency between the inputs and the rule's antecedent. The result of this step is a (reshaped) fuzzy set for each rule. Possible operators for the reshaping method are Truncate (by default) and Multiplication. Consider, for example, the rule at the top. Its original consequent is the fuzzy set "Good suitability" with membership function 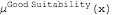 . The computation would be:
. The computation would be: 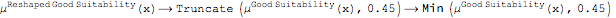 .
.
3. Aggregate all the reshaped consequents. The result of this step is one fuzzy set (labeled "Aggreg. Suitability"), which is the union of all the reshaped consequents. Possible operators for the aggregation are the Max, the probabilistic sum (ProbOr[a,b]:=a+b-ab) and the sum clipped at 1 (ClippedSum).
4. Defuzzify the aggregated fuzzy set. The defuzzification reduces the aggregated fuzzy set to one single number. Possible defuzzification methods are: center of gravity (COG), first of maxima (FOM), last of maxima (LOM), middle of maxima (MOM) and mean of maxima (MeOM).
If you want to use Mamdani (or max-min) inference, choose "Min" for logical AND, "Max" for logical OR, "Truncate" as "Reshaping method"," Max" as "Aggregation method", and "COG" as "Defuzzification method".
Reference
[1] G. J. Klir and B. Yuan, Fuzzy Sets and Fuzzy Logic: Theory and Applications, Upper Saddle River, New Jersey: Prentice Hall PTR, 1995.
Permanent Citation