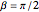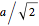Influence of a Moving Nodal Point on the "Causal Trajectories" in a Quantum Harmonic Oscillator Potential

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
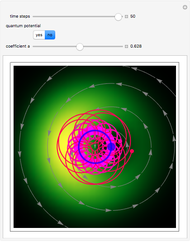
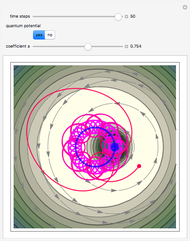
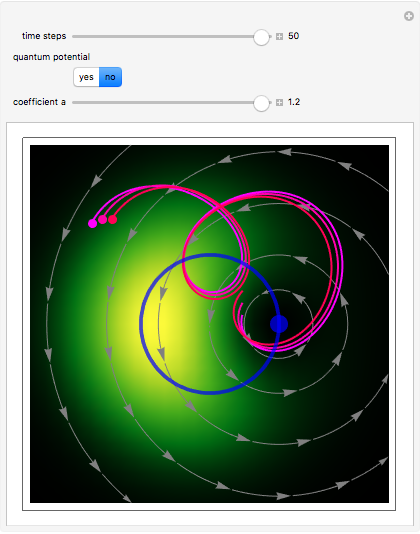
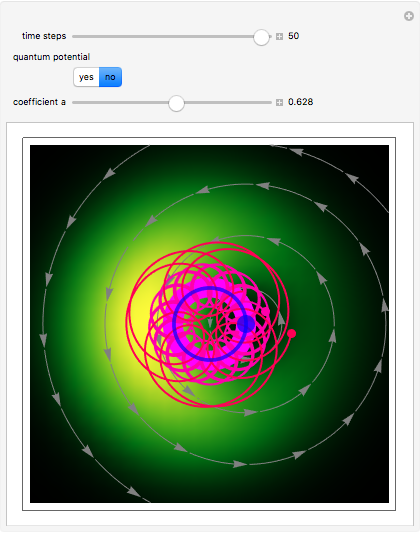
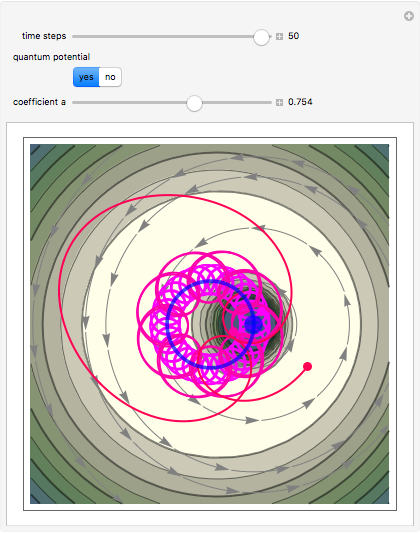
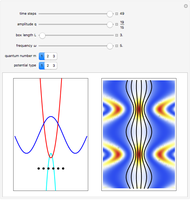
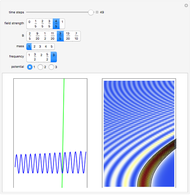
Chaotic motion in the vicinity of a moving quantum nodal point is studied in the framework of the de Broglie–Bohm trajectory method of quantum mechanics. Chaos emerges from the sequential interaction between the quantum path with the moving nodal point depending on the distance and the frequencies between the quantum particles and their initial positions [1]. Here, chaotic motion means the exponential divergence of initially neighboring trajectories.
[more]
Contributed by: Klaus von Bloh (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration studies a normalized superposition of ground state and a degenerate first excited state with a constant relative phase shift of an uncoupled isotropic harmonic oscillator in two dimensions. We assume commensurable frequencies, that is, a minimum common multiple period  exists. The squared wavefunction and therefore the nodal point have period
exists. The squared wavefunction and therefore the nodal point have period 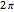 . The coefficient
. The coefficient  from the wavefunction governs the diameter of the orbit of the nodal point. The wavefunction obeys the Schrödinger equation:
from the wavefunction governs the diameter of the orbit of the nodal point. The wavefunction obeys the Schrödinger equation:
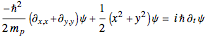 ,
,
with 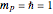 ,
, 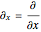 , and so on. The normalized wavefunction for this Demonstration is:
, and so on. The normalized wavefunction for this Demonstration is:
 ,
,
with the eigenfunctions 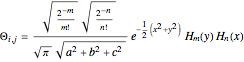 , where
, where  are the Hermite polynomials,
are the Hermite polynomials, 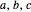 are arbitrary constants (here:
are arbitrary constants (here: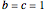 ),
),  are constant phase shifts, and the quantum numbers
are constant phase shifts, and the quantum numbers 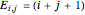 with
with 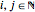 . The velocity field
. The velocity field 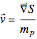 is calculated from the gradient of the phase from the total wavefunction in the eikonal form
is calculated from the gradient of the phase from the total wavefunction in the eikonal form 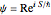 . For this Demonstration the velocity is:
. For this Demonstration the velocity is:
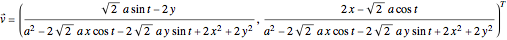 .
.
The quantum potential is:
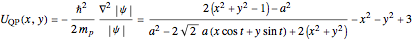 .
.
In the program, if PlotPoints, AccuracyGoal, PrecisionGoal, and MaxSteps are increased, the results will be more accurate.
References
[1] C. Efthymiopoulos, C. Kalapotharakos, and G. Contopoulos, "Origin of Chaos near Critical Points of the Quantum Flow," Physical Review E 79, 2009 pp. 036203-1–036203-18. doi:10.1103/PhysRevE.79.036203, arXiv: 0903.2655 [quant-ph].
[2] A. J. Makowski and M. Frackowiak, "The Simplest Non-trivial Model of Chaotic Causal Dynamics," Acta Physica Polonica B 32, 2001 pp. 2831–2842. arXiv: 0111155v1 [quant-ph].
Permanent Citation