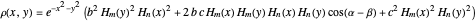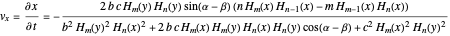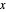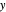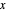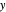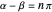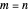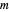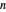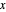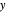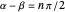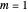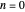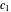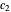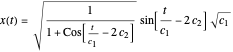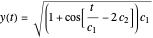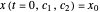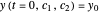Influence of the Relative Phase in the de Broglie-Bohm Theory

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
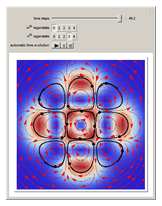
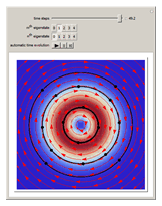
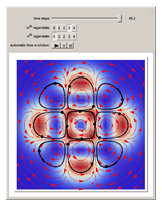
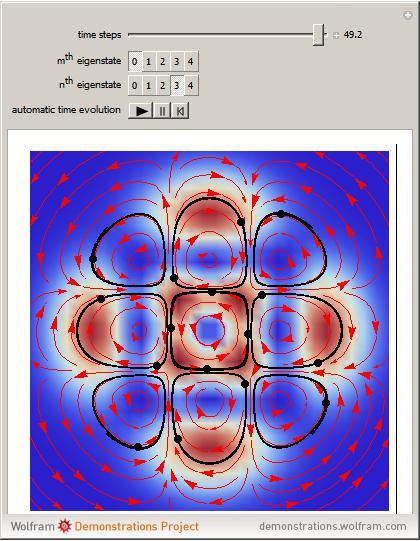
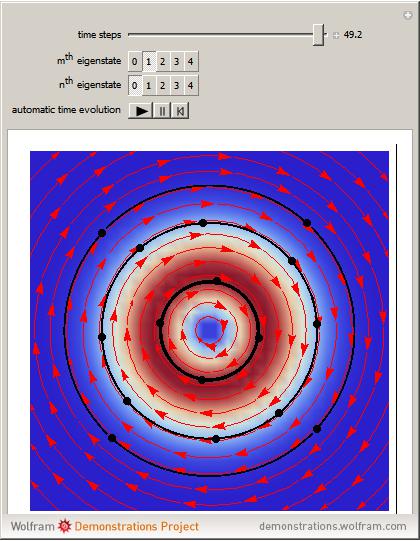
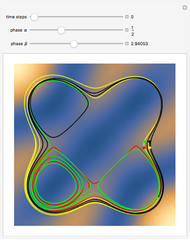
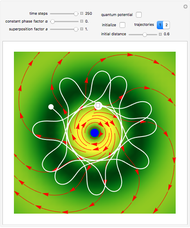
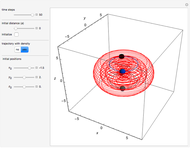
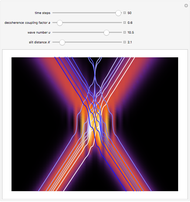
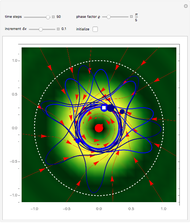
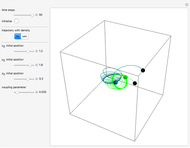
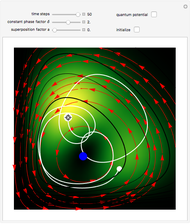
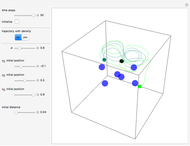
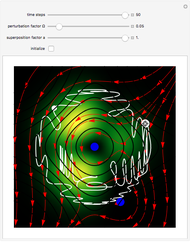
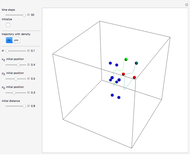
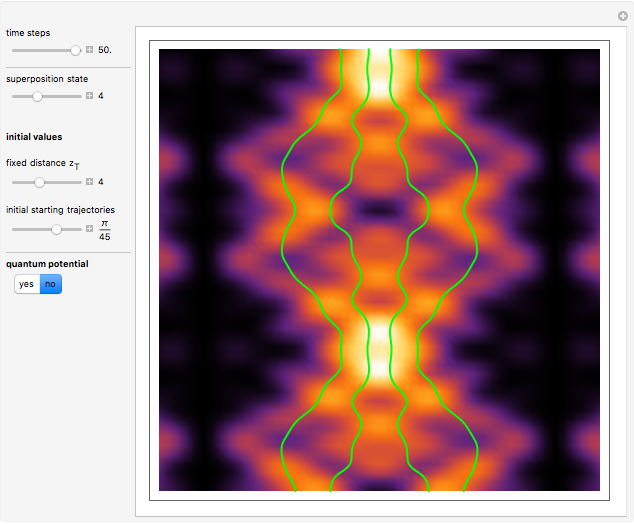
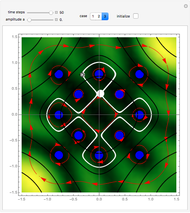
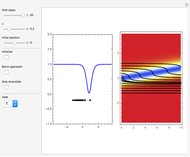
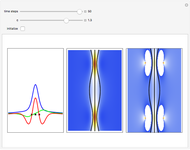
Does the possibility exist for motion of a quantum particle to occur when the particle density, given by the square of the Schrödinger wavefunction, is not time-dependent? This question is answered in this Demonstration. A system with two degrees of freedom assigned by a superposition of two stationary eigenfunctions that has commensurate energy eigenvalues can exhibit motion in the associated de Broglie–Bohm theory, provided that the constant phases 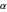 and
and 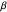 are not zero or integer multiples of
are not zero or integer multiples of 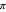 . The origin of the motion lies in the relative phase of the total wavefunction, which has no classical analogue in particle mechanics. As an example a wavefunction for a quantum isotropic harmonic oscillator is chosen:
. The origin of the motion lies in the relative phase of the total wavefunction, which has no classical analogue in particle mechanics. As an example a wavefunction for a quantum isotropic harmonic oscillator is chosen: 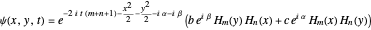 , where
, where 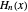 is the Hermite polynomial and
is the Hermite polynomial and  ,
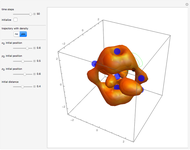
,  are arbitrary constants. In this case the squared wavefunction (particle density
are arbitrary constants. In this case the squared wavefunction (particle density  ) is not time-dependent:
) is not time-dependent:
Contributed by: Klaus von Bloh (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation