Wolfram Research

Mathematica MathWorld Wolfram Science More »

Integer Torus Maps


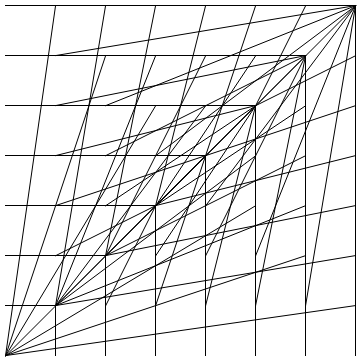
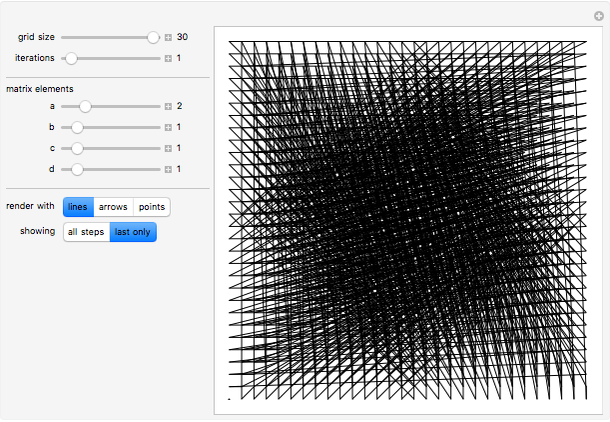
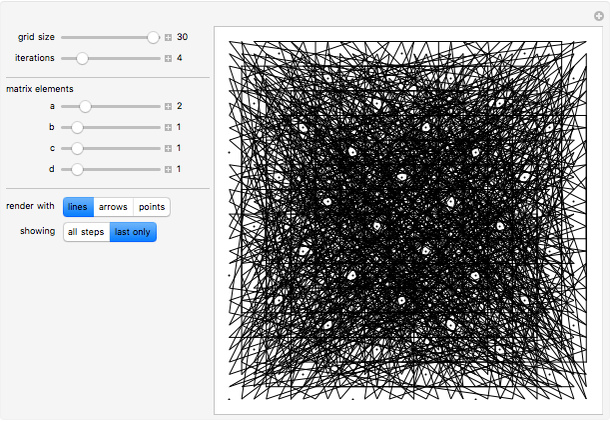
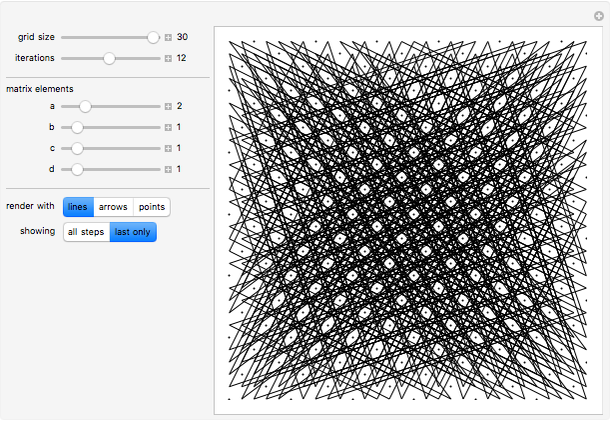
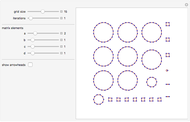
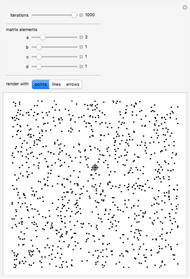
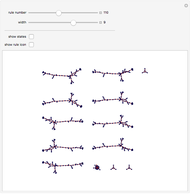
	Each point {x,y} in an integer grid of size n is joined to the point with coordinates obtained by iteratively applying the transformation Mod[{{a,b},{c,d}}.{x,y},n] the specified number of times.


	Contributed by: Stephen Wolfram

When the matrix {{a,b},{c,d}} is invertible, every point in the grid maps to a distinct point.

Higher-dimensional generalizations [of iterated maps] (NKS|Online)

"Integer Torus Maps" from The Wolfram Demonstrations Project
http://demonstrations.wolfram.com/IntegerTorusMaps/

Contributed by: Stephen Wolfram

Mathematica 7 Just Released--Get Mathematica Player 7 Free--Download Now

Related Topics

Browse all topics

Browse all education topics

Some Related Demonstrations

Share & Bookmark This Demonstration

Contribute

Powered by Wolfram Mathematica

Give us your feedback

	Source page:
	Email	Name (optional)
	Occupation (optional)	Organization (optional)
	I use Mathematica often occasionally never
	Country (optional) Remember me
	Note: Please do not include anything you consider confidential or proprietary. Your message and contact information may be shared with the author of any specific Demonstration for which you give feedback, but will not otherwise be published or distributed. Privacy Policy »

© 2009 Wolfram Demonstrations Project & Contributors

Wolfram Research

Site Index

RSS

Atom

Note: To run this Demonstration you need the free
Mathematica Player or Mathematica 7+