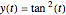Integrating across Singularities

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
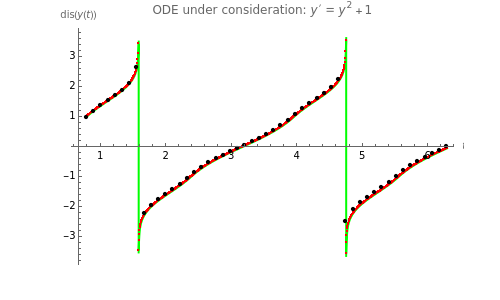
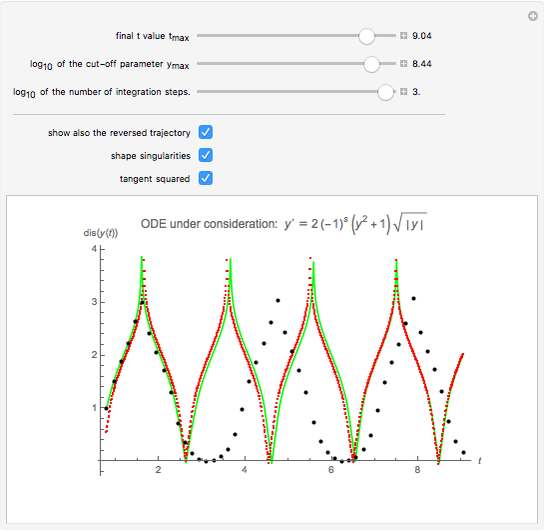
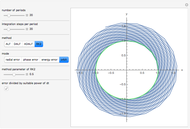
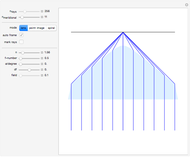
An initial value problem for a simple autonomous differential equation may develop singularities that prevent most time-discrete integrators from following the trajectory reliably. An example of this phenomenon is given by the ODE 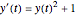 , for which the initial condition
, for which the initial condition  yields the solution
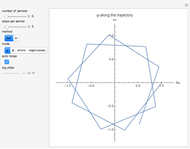
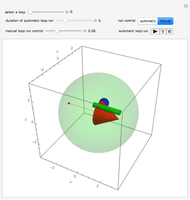
yields the solution 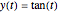 . This ODE describes the rotation of a rigid body around an axis fixed in space in a formalism that describes the attitude of the body by Euler–Rodrigues parameters (instead of, say, Euler angles or orthogonal matrices). Thus we have a setting that asks for continuing the trajectory across the singularities, which occur whenever
. This ODE describes the rotation of a rigid body around an axis fixed in space in a formalism that describes the attitude of the body by Euler–Rodrigues parameters (instead of, say, Euler angles or orthogonal matrices). Thus we have a setting that asks for continuing the trajectory across the singularities, which occur whenever  is
is  plus some integer multiple of
plus some integer multiple of  .
.
Contributed by: Ulrich Mutze (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
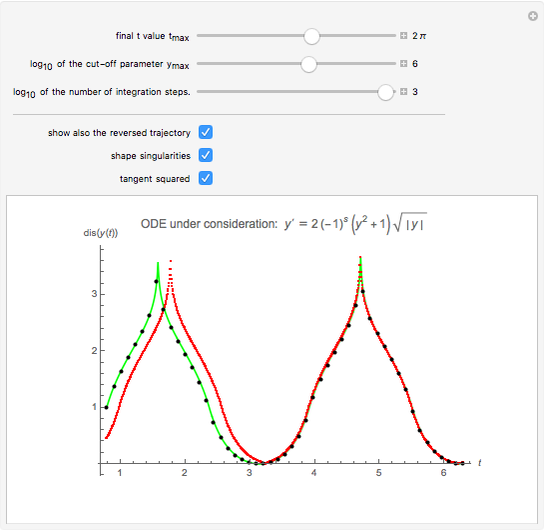
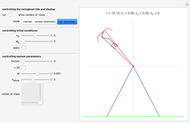
By checking the box "tangent squared", you replace the ODE 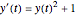 by an ODE that is constructed such that its solution is
by an ODE that is constructed such that its solution is 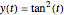 . For this
. For this  we have
we have 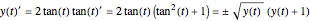 . The sign factor has to switch whenever the trajectory passes a singularity and also when
. The sign factor has to switch whenever the trajectory passes a singularity and also when 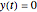 . As the program shows, the asynchronous leapfrog integrator can easily be made to do this switching. So it is not necessary to know in advance the
. As the program shows, the asynchronous leapfrog integrator can easily be made to do this switching. So it is not necessary to know in advance the  values for which switching has to take place.
values for which switching has to take place.
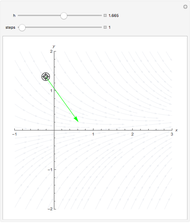
Snapshot 1:  adjusted for good representation of the exact solution
adjusted for good representation of the exact solution
Snapshot 2:  not so well adjusted; no good behavior of the reversed trajectory
not so well adjusted; no good behavior of the reversed trajectory
Snapshot 3:  set too large; complete disorder after the first singularity
set too large; complete disorder after the first singularity
References
[1] Ulrich Mutze, An Asynchronous Leap-Frog Method, 2008. http://www.ma.utexas.edu/mp_arc/c/08/08-197.pdf.
[2] Alternate link for [1]: http://www.ulrichmutze.de/articles/leapfrog4.pdf.
[3] Ulrich Mutze, On Vectors, Points, Rotations, and Rigid Bodies. http://www.ulrichmutze.de/pedagogic_stuff/geo_10.pdf.
Permanent Citation