Interpolating B-Spline Curves with Boundary Conditions
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
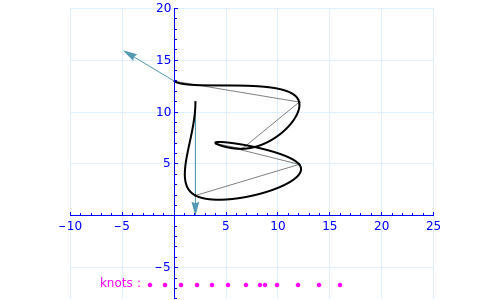
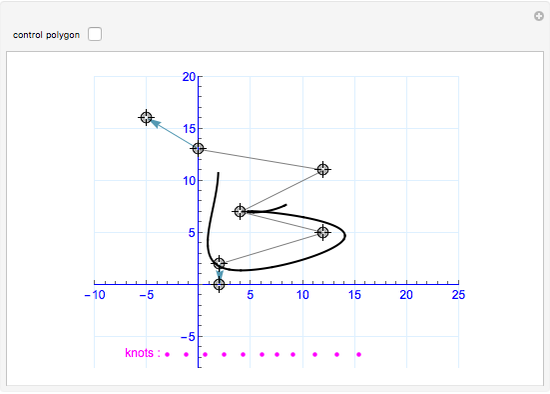
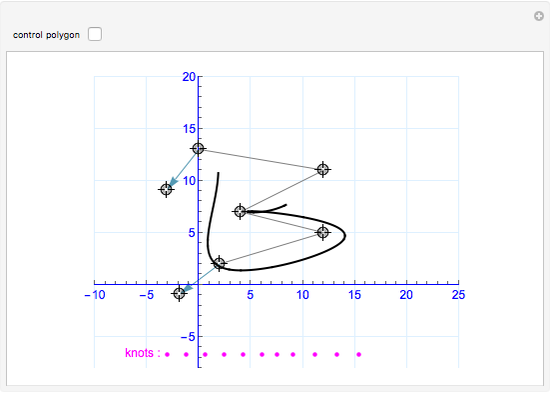
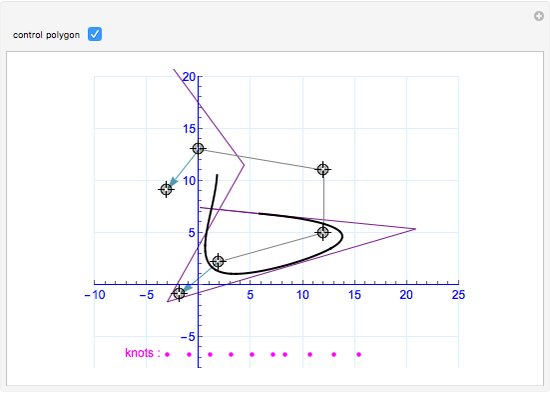
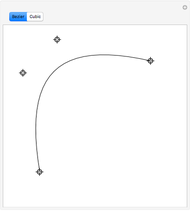
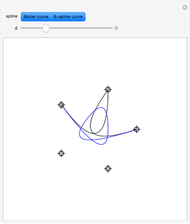
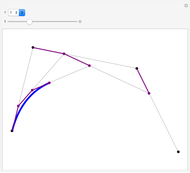
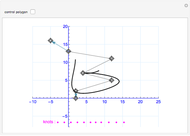
A B-spline curve is determined by interpolation points and the tangent vectors at both ends. There can be four to 12 locators; new ones are added at the end.
Contributed by: M. Szilvási-Nagy (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The control points of the nonuniform cubic B-spline curve are determined from the interpolation points and the boundary conditions. The first and last two control points are so-called phantom points, which are determined by the first-order boundary conditions. The computational method can be applied to three-dimensional curves, too.
B. K. Choi, W. S. Yoo, and C. S. Lee, "Matrix Representation for NURB Curves and Surfaces," Computer-Aided Design, 22(4), 1990 pp. 235–239.
G. E. Farin, Curves and Surfaces for Computer-Aided Geometric Design, San Diego, CA: Academic Press, 1988.
Permanent Citation
"Interpolating B-Spline Curves with Boundary Conditions"
http://demonstrations.wolfram.com/InterpolatingBSplineCurvesWithBoundaryConditions/
Wolfram Demonstrations Project
Published: March 7 2011
Simple Spline Curves
Richard Phillips and Rob Morris
B-Spline Basis Functions
Tammo Jan Dijkema
Shaping a Tubular B-Spline Surface
M. Szilvási-Nagy
Interpolating the Hilbert Curve with a B-Spline
Michael Trott
Interactive Spline
Faisal Whelpley
Averaged Gosper Curves
Michael Trott
Bézier Curve by de Casteljau's Algorithm
Bruce Atwood
B-Spline Curve with Knots
Yu-Sung Chang
Algorithm for Cubic Nonuniform B-Spline Curve Interpolation
Shutao Tang
Knot Vector Generation for B-Spline Interpolation
Isabelle Cattiaux-Huillard and Gudrun Albrecht
