Interpolating Vertical Segments

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
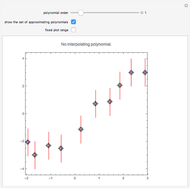
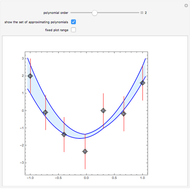
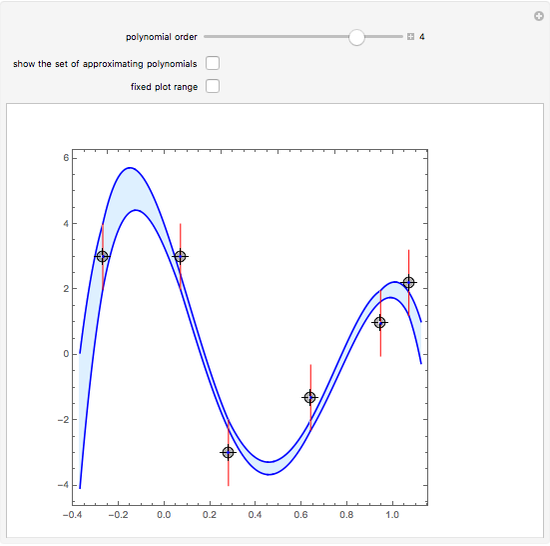
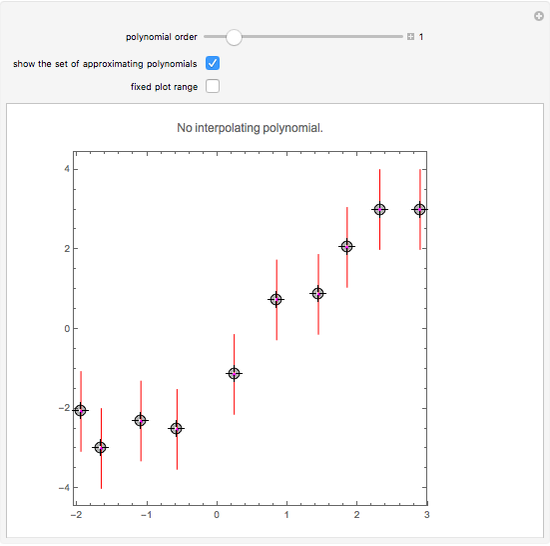
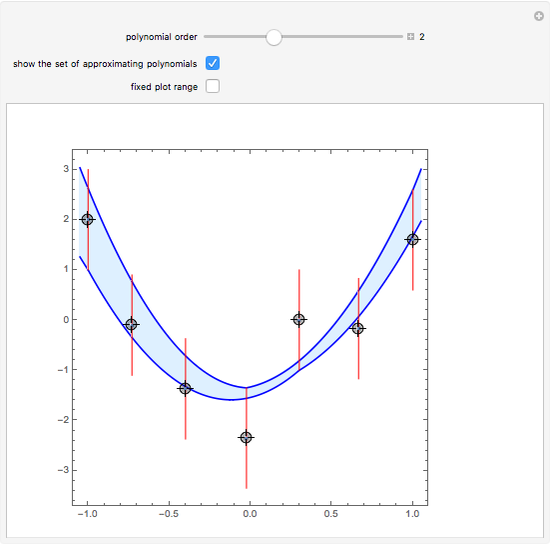
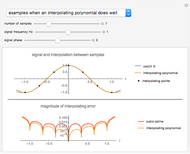
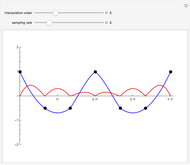
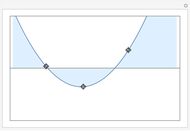
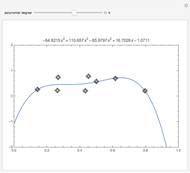
This Demonstration shows the polynomials of degree 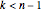 that interpolate a given set of
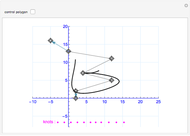
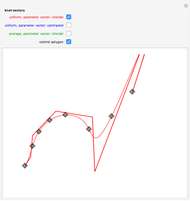
that interpolate a given set of  vertical segments in the plane. If there is no interpolating polynomial of a particular degree, the set of all approximating polynomials of the same degree can be represented by its boundary (colored in magenta).
vertical segments in the plane. If there is no interpolating polynomial of a particular degree, the set of all approximating polynomials of the same degree can be represented by its boundary (colored in magenta).
Contributed by: Evgenija D. Popova and Radostin Surilov (March 2011)
Open content licensed under CC BY-NC-SA
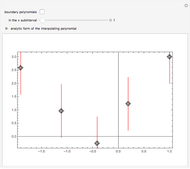
Snapshots
Details
Given a set of  distinct real numbers (input data)
distinct real numbers (input data) 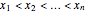 and a set of
and a set of  (output) measurements that are unknown but bounded in compact real intervals
(output) measurements that are unknown but bounded in compact real intervals 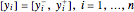 . The pair
. The pair 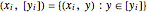 is a vertical segment in the
is a vertical segment in the  -
- plane
plane We assume that the input data are in the interval
We assume that the input data are in the interval 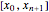 with
with 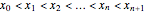 .
.
For a given set of  vertical segments and an integer
vertical segments and an integer 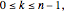
 represents the set of all real algebraic polynomials of degree
represents the set of all real algebraic polynomials of degree  that interpolate the vertical segments
that interpolate the vertical segments  , that is,
, that is, 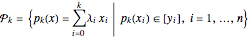 . The set
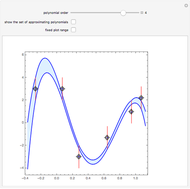
. The set  of interpolating polynomials is represented in blue; its boundary consists of piecewise real interpolating polynomials in each subinterval
of interpolating polynomials is represented in blue; its boundary consists of piecewise real interpolating polynomials in each subinterval 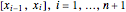 ; see also [2].
; see also [2].
If, for a set of vertical segments, there is no interpolating polynomial of a particular degree, the set of all approximating polynomials of the same degree can be represented by its boundary (colored in magenta).
Details about the theory and implementation algorithms can be found in [1].
References
[1] S. M. Markov and E. D. Popova, "Linear Interpolation and Estimation Using Interval Analysis", Bounding Approaches to System Identification, New York: Plenum Press, 1996 pp. 139–157.
Permanent Citation