Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Intersection of a Plane and a Tetrahedron

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

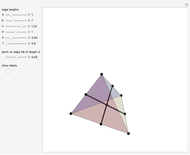
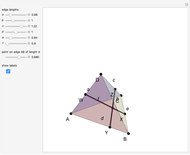
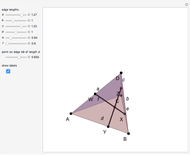
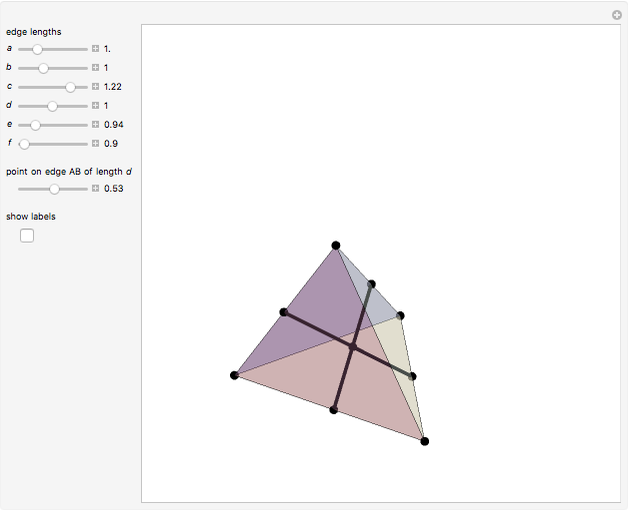
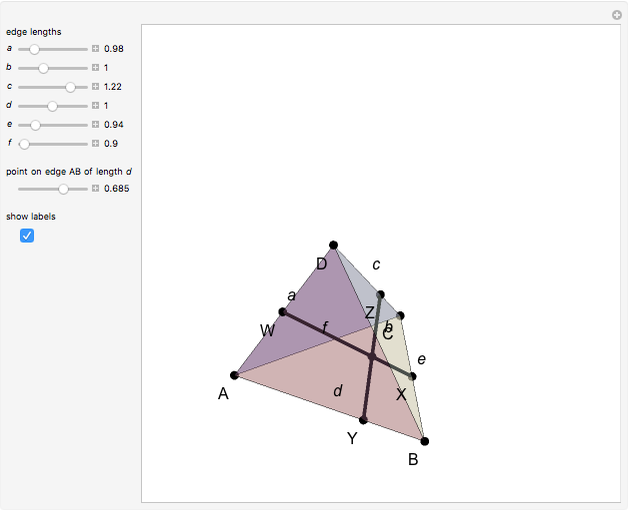
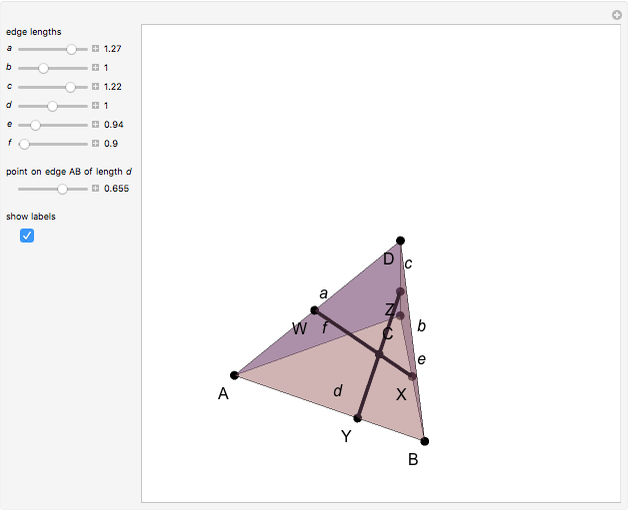
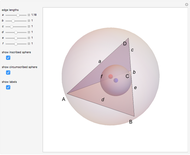
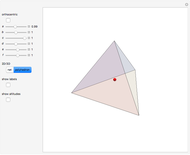
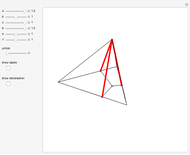
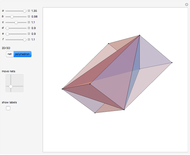
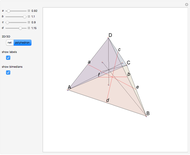
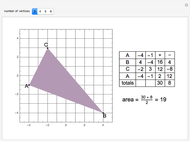
Let 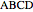be a tetrahedron and let and 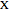be the midpoints of the edges 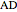and 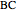. Let a plane that contains the line 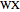intersect the edges 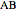and at points 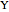and . Then 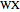bisects .

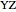Contributed by: Izidor Hafner (March 2017)
Open content licensed under CC BY-NC-SA

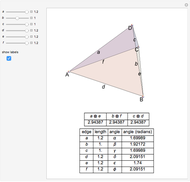
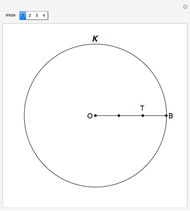
Snapshots

Details

A proof is described in [1, p. 126].

Reference

[1] V. V. Prasolov and I. F. Sharygin, Problems in Stereometry (in Russian), Moscow: Nauka, 1989.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send