Inverse Function of a Trigonometric Function Game

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
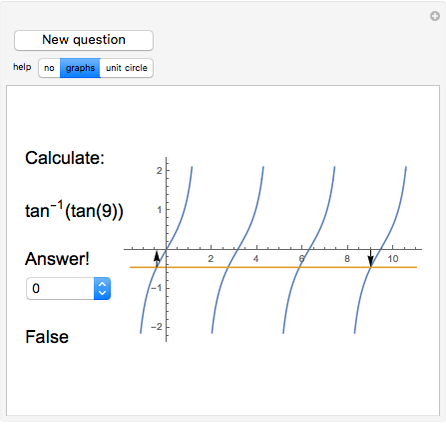
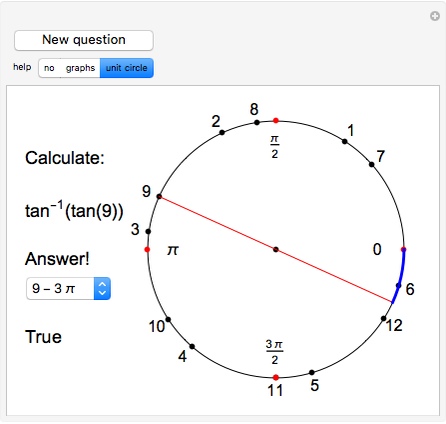
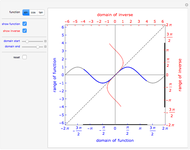
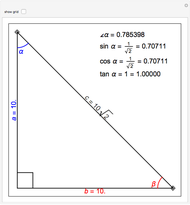
This Demonstration provides a game for the exact calculation of  for trigonometric functions.
for trigonometric functions.
Contributed by: Izidor Hafner (November 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
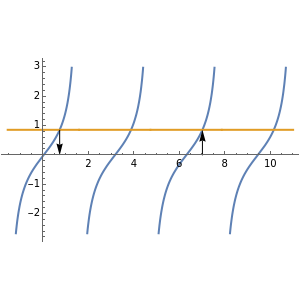
The trigonometric functions are not invertible because they are not one-to-one (their graphs fail a horizontal line test). However, by restricting their domains, one can create restricted versions of these functions that are invertible, and the inverse trigonometric functions are thus defined. For example, the function 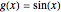 is not one-to-one, but the function
is not one-to-one, but the function 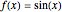 ,
,  , is one-to-one, and the function
, is one-to-one, and the function 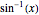 is the inverse of
is the inverse of 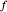 . For any function
. For any function 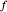 ,
, 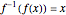 , but since
, but since 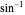 is not really the inverse of
is not really the inverse of  , but of its restriction, it is possible to have
, but of its restriction, it is possible to have 
Permanent Citation