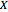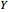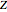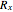Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Inverse Kinematics for a Robot Manipulator with Six Degrees of Freedom

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

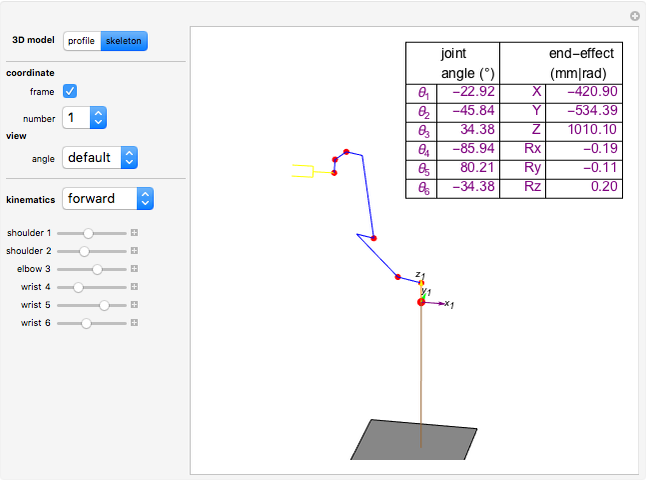
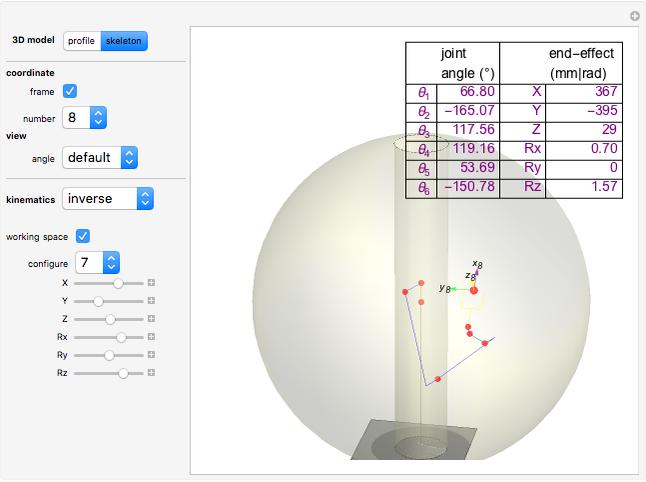
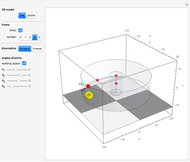
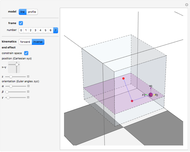
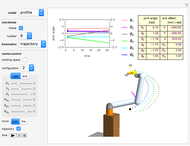
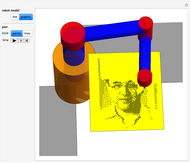
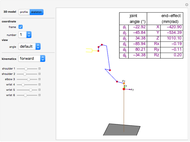
The inverse kinematics problem for serial manipulators is central in the automatic control of robot manipulators. Given the pose of the end effector, the problem corresponds to computing the joints rotation for that pose. (Pose is the robotics term for the combination of position and orientation.)

[more]

This Demonstration shows a forward kinematic model of an industrial manipulator using D-H (Denavit–Hartenberg) notation to propagate links transformations from base to end effector. To solve inverse kinematics problem, this demonstration shows a close-form solution with 8 configures. The end effector’s are free to move for all 6 degrees of freedom and for position, and and for orientation. A simple trajectory generation is introduced to make the robot move from one point to another along a straight line.

[less]

Contributed by: Frederick Wu (September 2015)
Open content licensed under CC BY-NC-SA

Snapshots

Details

References

[1] M. Raghavan and B. Roth, "Kinematic Analysis of the 6R Manipulator of General Geometry," Proceedings of the Fifth International Symposium on Robotics Research (H. Miura, ed.), Cambridge, MA: MIT Press, 1990 pp. 263–269. dl.acm.org/citation.cfm?id=112715&CFID=542850644&CFTOKEN=11490130.

[2] D. Manocha and J. F. Canny, "Efficient Inverse Kinematics for General 6R Manipulators," IEEE Transactions on Robotics and Automation, 10(5), 1994 pp. 648–657. doi:10.1109/70.326569.

[3] R. N. Jazar, Theory of Applied Robotics (Kinematics Dynamics and Control), 2nd Ed., Springer: New York, 2010, pp. 341–356.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send