Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

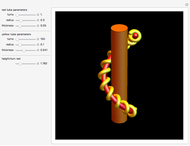
Inverse Stereographic Projection of the Logarithmic Spiral

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

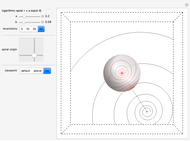
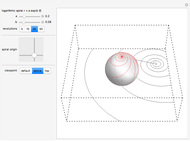
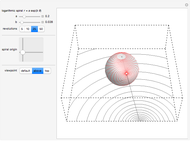
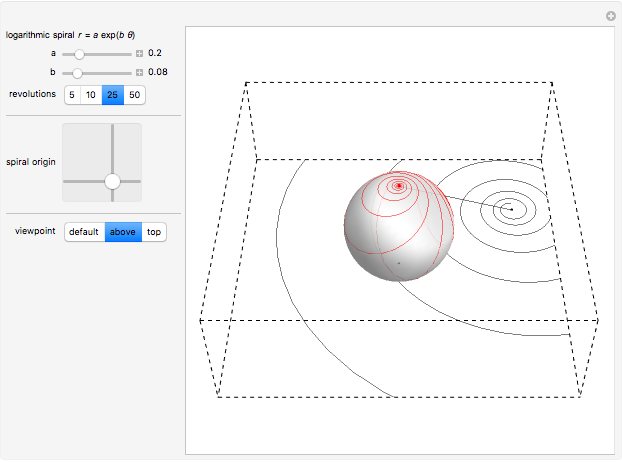
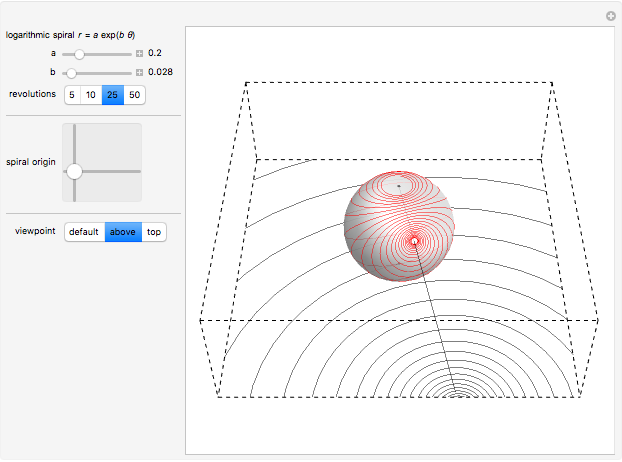
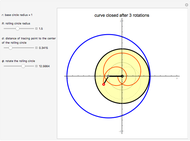
This Demonstration shows the inverse stereographic projection of a logarithmic spiral onto the unit sphere. You can move the spiral in the plane; it maps on the sphere as a loxodrome.

Contributed by: Erik Mahieu (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The inverse stereographic projection of the point 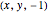to the unit sphere is the point .

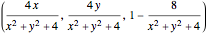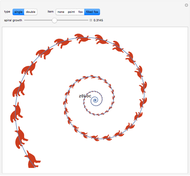
A logarithmic or equiangular spiral is defined as a two-dimensional curve that cuts all radial lines at a constant angle. Its polar equation is given by .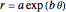

A loxodrome on a sphere (spherical spiral) is a curve that cuts all meridians at the same angle. The stereographic projection of a loxodrome is a logarithmic spiral.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send