Inversive Geometry I: Basic Properties of Inversion

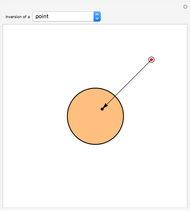
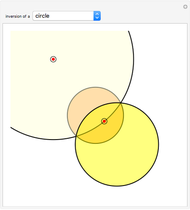
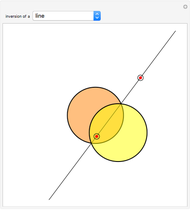
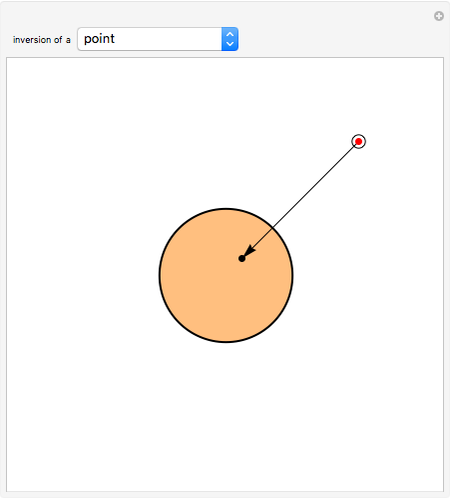
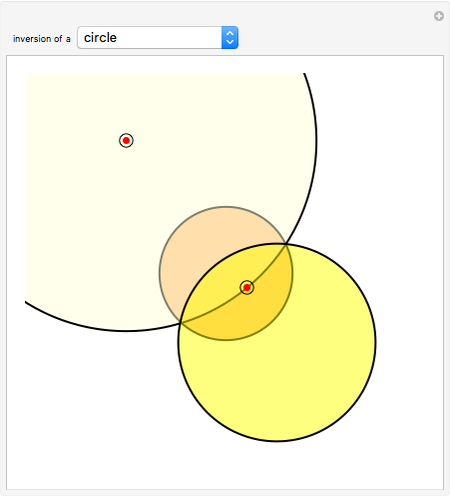
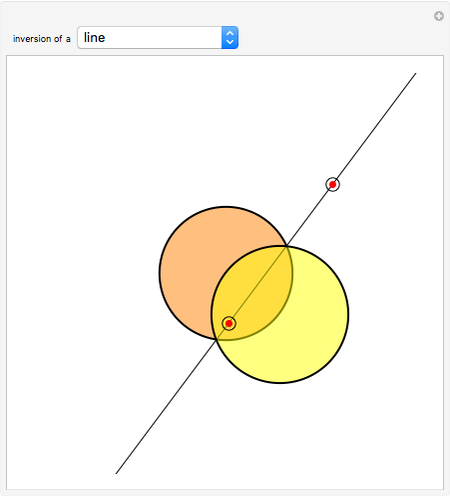
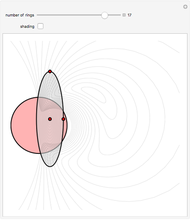
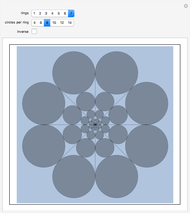
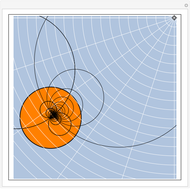
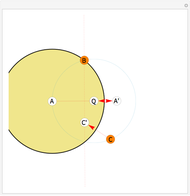
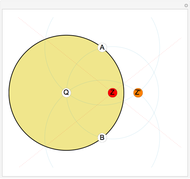
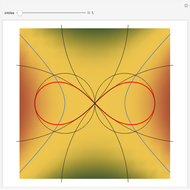
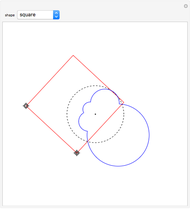
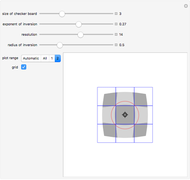
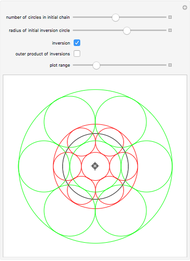
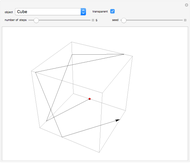
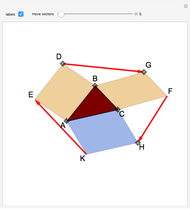
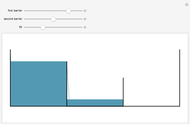
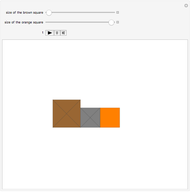
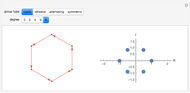
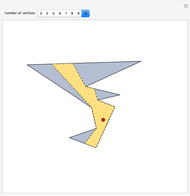
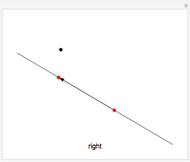
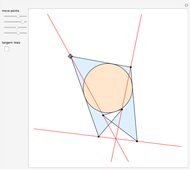
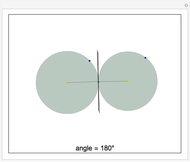
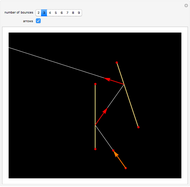
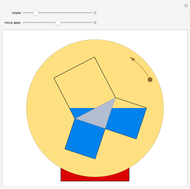
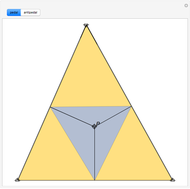
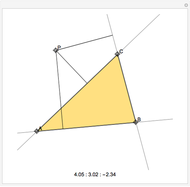
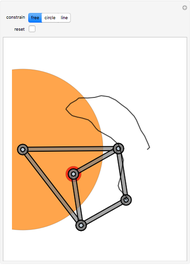
Given a fixed circle (depicted in orange) of center and radius , inversion is a mapping fixing it and swapping its interior and exterior in such a way that the product of the distances to of a point and its image (both in line with ) is equal to . This Demonstration shows the effect of inversion on points, circles, lines, circles passing through , vertices of triangles and squares, and the interior of triangles. Handles are provided (in red double circles) to let you vary these shapes.