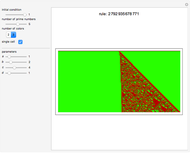
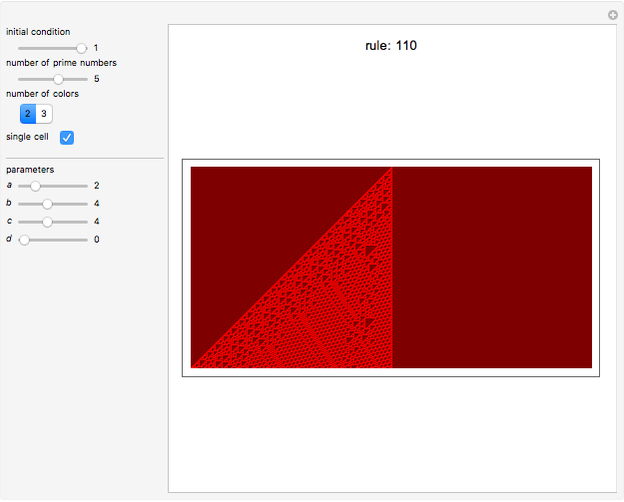
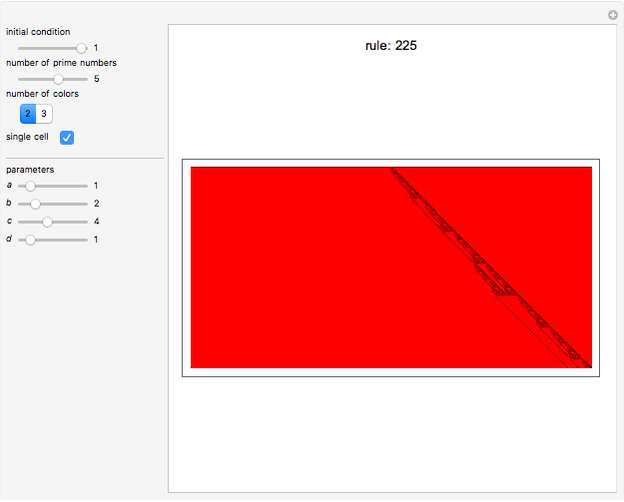
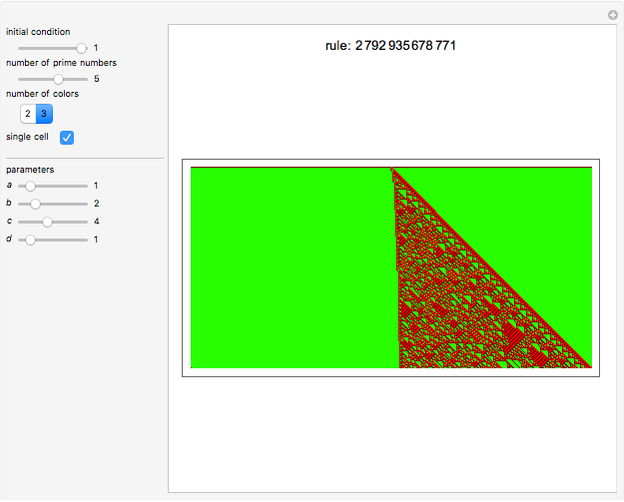
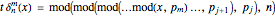Iota-Delta Function for Generating Cellular Automata

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
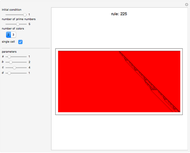
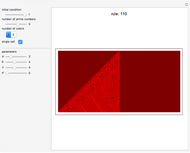
Universality has always played a major role in every branch of science. In particular, universality in cellular automata (CA) and computational systems has been explored extensively, especially the elementary CA (ECA) rule 110 and its properties. Instead of considering universal rules, one may think of universal functions that, when applied to the cellular automaton net, generate every CA. This approach asks that one imagine the cellular automaton net as a functional space whose values are determined by means of the conjectured function and its parameters. Following this idea, different functional parameters should generate different CAs. This universal function, the iota-delta function, has been proved to exist and is defined as follows:
[more]
Contributed by: André Luís Brasil Cavalcante, Luan Carlos de Sena Monteiro Ozelim, and Lucas Parreira de Faria Borges (July 2012)
Advisor: Todd Rowland
Open content licensed under CC BY-NC-SA
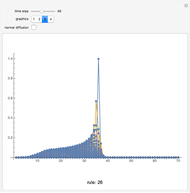
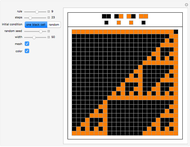
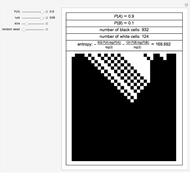
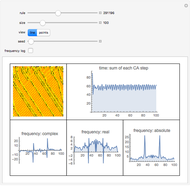
Snapshots
Details
References
[1] L. C. S. M. Ozelim, A. L. B. Cavalcante, and L. P. F. Borges, "Continuum versus Discrete: A Physically Interpretable General Rule for Cellular Automata by Means of Modular Arithmetic," arXiv, 2012. arxiv.org/1206.2556.
[2] P.-J. Letourneau, "Statistical Mechanics of Cellular Automata with Memory," M.S. thesis, Department of Physics and Astronomy, University of Calgary, Canada, 2006. www.rule146.com/thesis/msc-thesis-letourneau-eca-memory.pdf.
[3] S. Wolfram, A New Kind of Science, Champaign, IL: Wolfram Media, Inc., 2002.
[4] Wolfram Science Summer School 2012. www.wolframscience.com/summerschool/2012 (NKS|Online).
Permanent Citation