Iso-Optic Plane of the Regular Tetrahedron

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
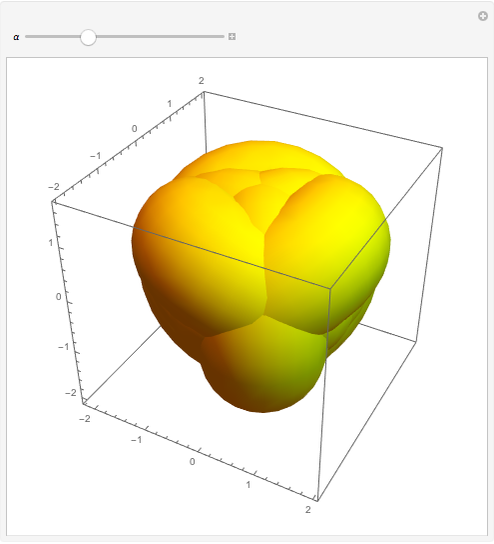
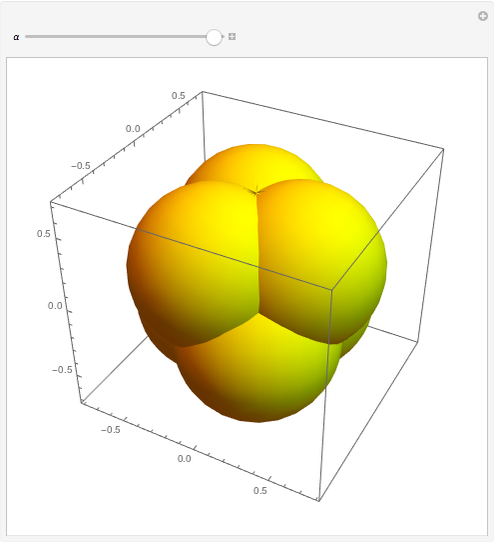
This Demonstration shows the points in space that subtend an angle  from a regular tetrahedron with vertices
from a regular tetrahedron with vertices  .
.
Contributed by: Géza Csima (June 2009)
Suggested by: Jenő Szirmai
Additional contributions by: János Tóth
Open content licensed under CC BY-NC-SA
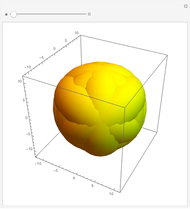
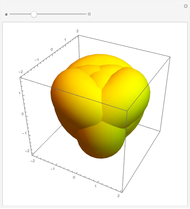
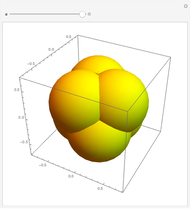
Snapshots
Details
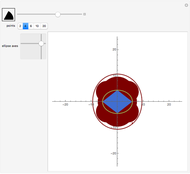
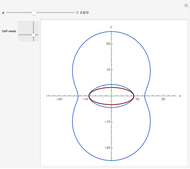
In the plane, it is easy to show those points from which a segment subtends an angle  because they form a circle. However, for a segment in space, the points subtended form a torus, where
because they form a circle. However, for a segment in space, the points subtended form a torus, where 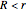 (i.e., the torus intersects itself). The long derivation for a tetrahedron is not shown; only the result is used.
(i.e., the torus intersects itself). The long derivation for a tetrahedron is not shown; only the result is used.
You can select  between
between 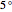 and
and 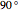 .
.
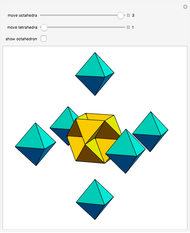
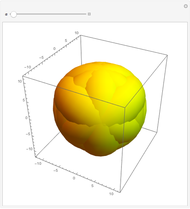
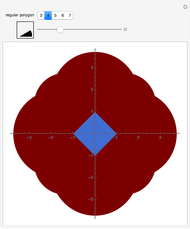
In the first snapshot you can see that if  is small, the figure looks like a sphere; the second snapshot shows the general case; and in the third snapshot spheres appear because
is small, the figure looks like a sphere; the second snapshot shows the general case; and in the third snapshot spheres appear because  is
is 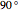 .
.
Permanent Citation