Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Isocosts, Isoquants, Isocline Lines, and Scale Lines for Homogeneous (Cobb-Douglas) Functions

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

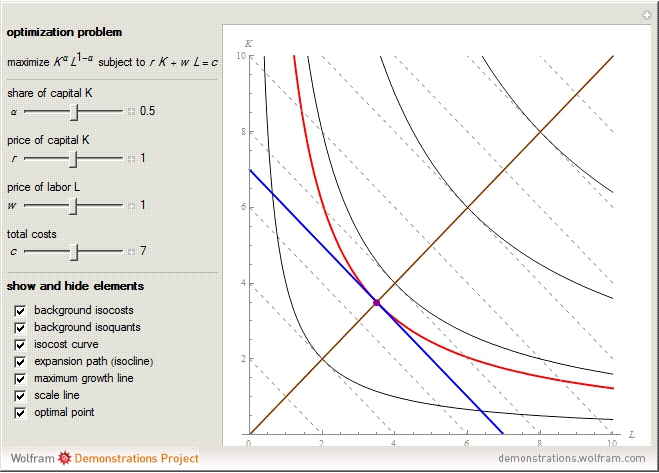
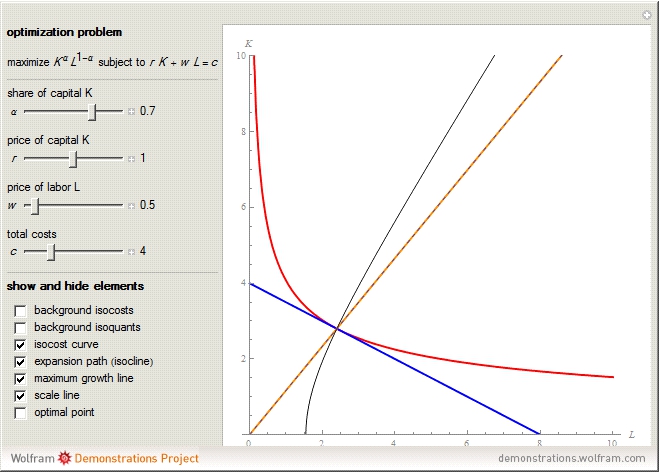
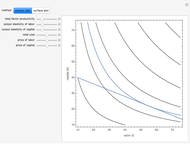
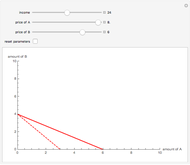
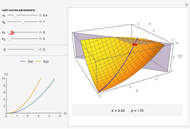
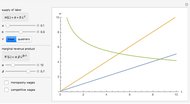
This Demonstration compares graphically such concepts as isocosts, isoquants, isocline lines (also known as expansion paths), and scale lines in the case of a homogeneous production function in its simple Cobb–Douglas form, . You can vary the linear budget constraint.

[more]

Production function is one of the key concepts in economics. In the most general terms, it maps inputs into outputs. One of the well-studied and often-used production functions is the Cobb–Douglass function, named after two coauthors who proposed it in 1928. The Cobb–Douglass function belongs to a class of homogeneous functions.

In order to maximize the output given the resource (budget) constraint, we can find an optimum combination of resources (inputs). The resource constraint is reflected by the isocost line that is tangent to the respective isoquant line (the contour line of production function passing through the optimal point). There are different trajectories (paths, lines) through which we may change resource combinations. Some of them possess interesting properties and are used to characterize the production function.

Scale lines are lines with a constant average rate of resources (K/L). Isocline lines pass through all points with the same substitution rate of resources (dK/dL). In general they differ from the production function fastest growth path reflected by a stream line.

[less]

Contributed by: Timur Gareev (July 2015)
Open content licensed under CC BY-NC-SA

Snapshots

Details

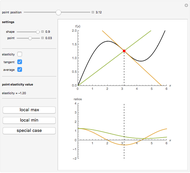
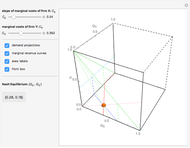
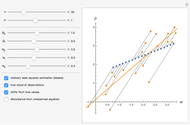
The Demonstration lets you study the behavior of different lines by switching them on/off in the graph. The basic isoquant comes from solving an optimization problem for a given isocost that serves as a constraint.

The optimal solution gives the optimal point that is used to build all the important lines simultaneously passing through the point, including a scale line, an isocline line, and a stream line (tangent to the gradient at the point and orthogonal to the isoquant). All three lines coincide for the special case of the Cobb–Douglas function with . Isocline lines and scale lines coincide for a homogeneous (i.e. Cobb–Douglas) function.

Nonetheless, it is important to distinguish between the concepts, as they differ in the case of nonhomogeneous functions. Any scale line starting from the origin unifies points with the same slope (meaning the same proportion of production factors). Each isocline line reflects all points with the same slope of gradients (the term "isocline lines" is also known as "expansion path" in economics). The maximum growth line (or stream line) shows the optimal path defined by changing the slope of the gradient.

Reference

[1] J. Whitehead, Microeconomics: A Global Text (ebook edition), New York: Routledge, 2014 pp. 147–148.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send