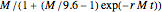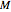Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Iterations of Some Algorithms for Nonlinear Fitting

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

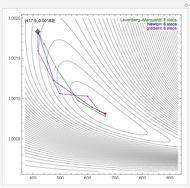
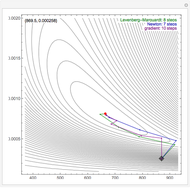
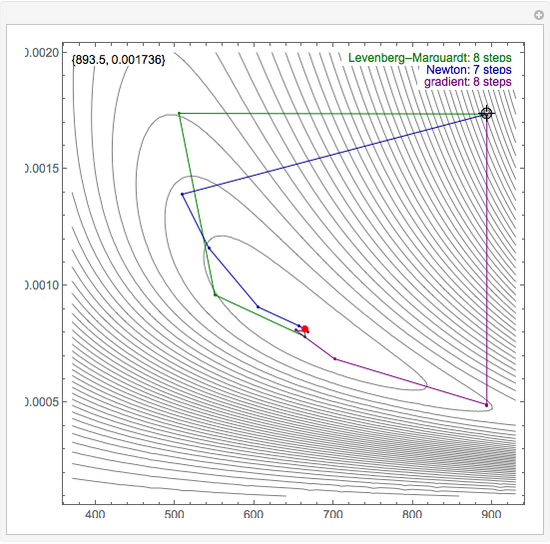
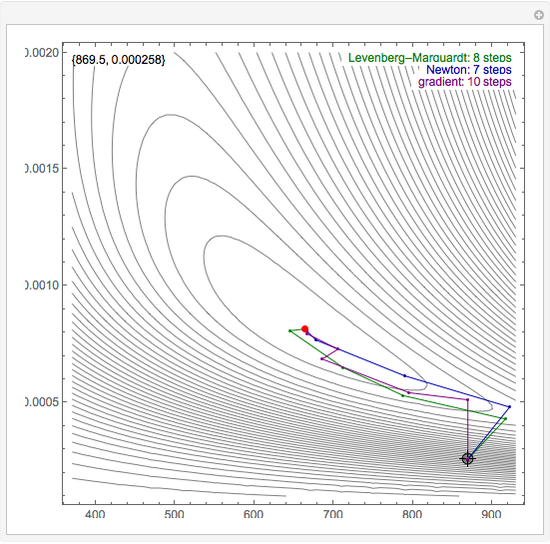
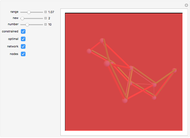
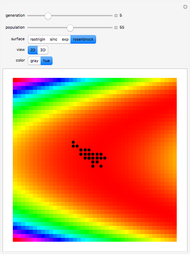
By dragging the starting point with the locator, you can see how three nonlinear fitting algorithms proceed and how many steps they need. The three algorithms considered are the Levenberg–Marquardt, Newton, and gradient methods.

[more]

In our example, we fit a logistic model to a yeast culture data [1]. The data is as follows: 9.6, 18.3, 29.0, 47.2, 71.1, 119.1, 174.6, 257.3, 350.7, 441.0, 513.3, 559.7, 594.8, 629.4, 640.8, 651.1, 655.9, 659.6, 661.8.

These figures are the size of the yeast culture measured at 0, 1, 2, …, 18 (hours). The logistic model is . The background plot is a contour plot of the sum of the squared residuals with respect to and . The solution of the fitting problem is the minimum point of the sum of the squared residuals (shown in red).

[less]

Contributed by: Heikki Ruskeepää (February 2012)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Reference

[1] R. Pearl, "The Growth of Populations," Quarterly Review of Biology, 2(4), 1927 pp. 532–548.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send