Iterative Polygon Simplification

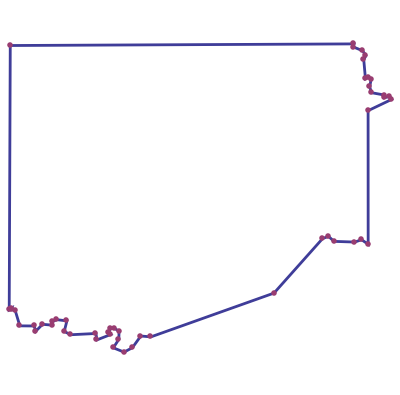
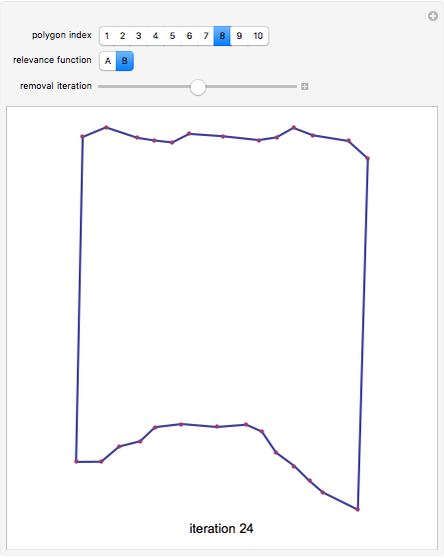
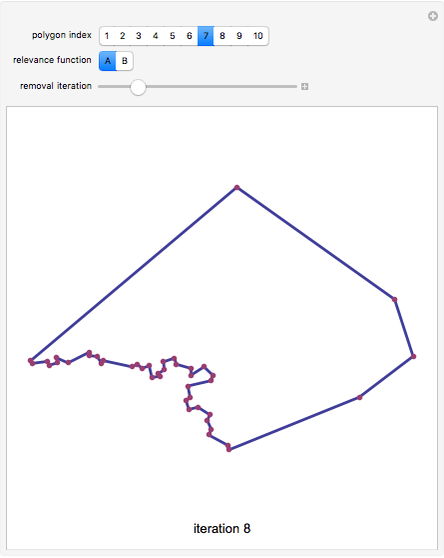
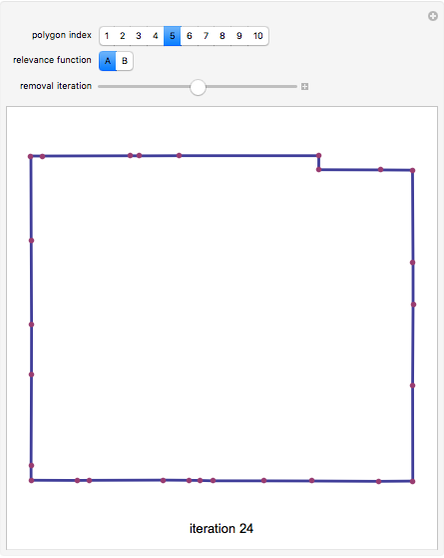
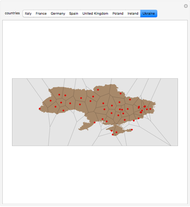
Polygons such as those created by geographic information systems are sometimes represented by data that is larger than necessary for relevant computations. This Demonstration shows how the representation of a polygon can be compressed. Although the compression is sometimes not lossless, for many practical purposes the shape or icon that results conveys adequate information for visualization, recognition, and computation. You select one of ten polygons that describe the shape of Texas counties using 50 points. You also select from two methodologies for determining the "relevance" of each vertex in the polygon. You can then drag the "removal iteration" slider to the right and see the least "relevant" points found by the selected method sequentially removed.

Contributed by: Seth J. Chandler

Show Initialization Code

(32 lines omitted)

"Method A" tends to result in more angular shapes than "method B", which tends to produce "curvier" shapes.

The algorithms used to determine the relevance of a vertex in a polygon are set forth and illustrated in D. J. Lee, S. Antani, and L. R. Long, "Similarity Measurement Using Polygon Curve Representation and Fourier Descriptors for Shape-Based Vertebral Image Retrieval," in Proceedings of SPIE--Volume 5032, Medical Imaging 2003: Image Processing (M. Sonka & J. M. Fitzpatrick, eds.), 2003 pp. 1283–1291.

The implementation of the simplification algorithm used in this Demonstration achieves needed speed by using the Mathematica compiler and by recognizing that most of the computed "relevance" values for each vertex are unaffected when a vertex is removed. Only the relevances of the neighboring vertices are potentially affected. Thus, the data structure used in this implementation stores a cache of computed relevance values and only computes new values when the removal of a vertex so requires. A compressed representation of the iterative simplification of the polygon is achieved by using an analogy to the GraphicsComplex command in Mathematica. The algorithm stores the coordinates of all the original points in the polygon, the currently active points, and the sequence of removed vertices. This data structure permits the Mathematica Fold or FoldList commands to readily reconstruct how a shape was simplified.