Jacobi Polynomials in an Orthogonal Collocation Method

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
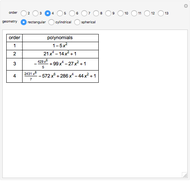
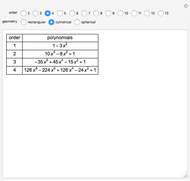
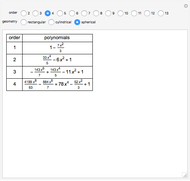
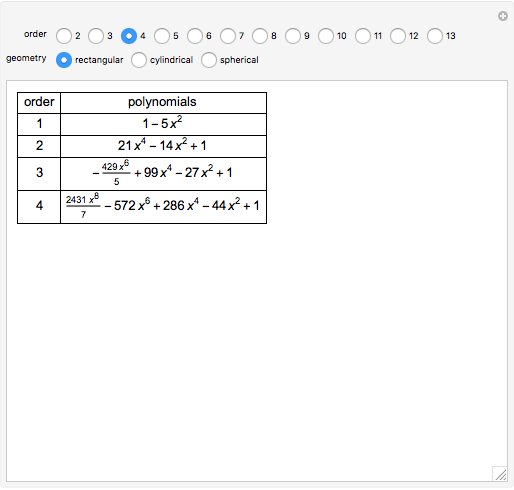
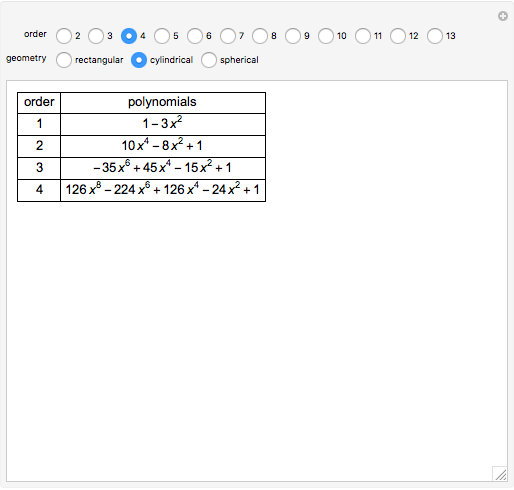
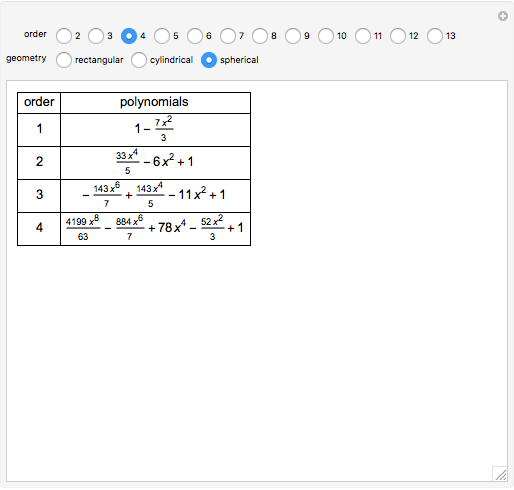
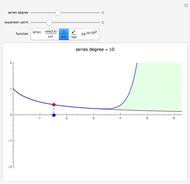
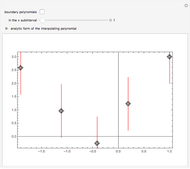
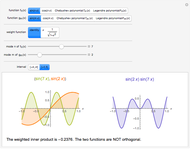
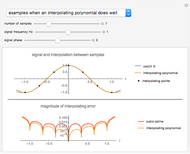
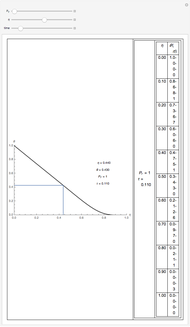
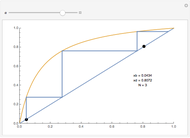
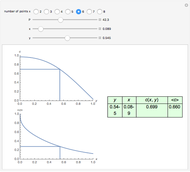
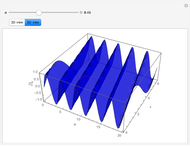
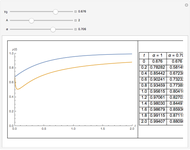
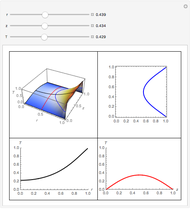
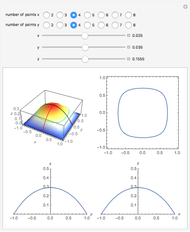
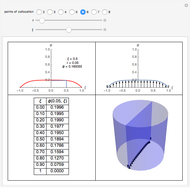
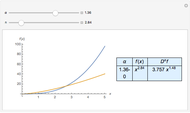
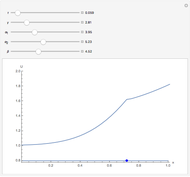
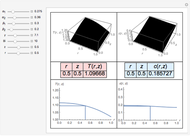
Partial differential equations in rectangular, cylindrical, and spherical coordinates with symmetric boundary conditions occur in many fields of science and engineering. It is often possible to solve such equations using an orthogonal collocation method with roots of Jacobi polynomials as the points of collocation.
Contributed by: Jorge Gamaliel Frade Chávez (March 2011)
Open content licensed under CC BY-NC-SA
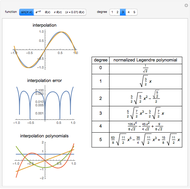
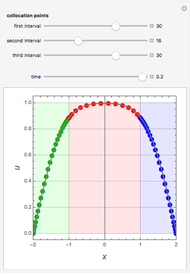
Snapshots
Details
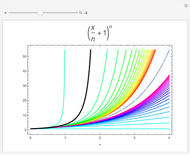
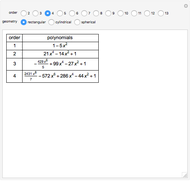
Symmetric Jacobi polynomials used in the orthogonal collocation method can be obtained from
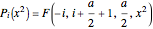 ,
,
where 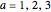 applies to a rectangular, cylindrical, or spherical coordinate, respectively,
applies to a rectangular, cylindrical, or spherical coordinate, respectively, 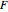 is the hypergeometric function,
is the hypergeometric function,  is the order in the polynomial,
is the order in the polynomial,  is the
is the  Jacobi polynomial, and
Jacobi polynomial, and  is the independent variable.
is the independent variable.
Reference: J. V. Villadsen and W. E. Stewart, "Solution of Boundary-Value Problems by Orthogonal Collocation," Chemical Engineering Science, 22, 1967 pp. 3981–3996.
Permanent Citation