Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

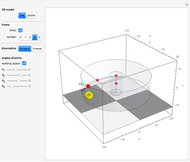
Joint Space and Tooling Space for Robot Motion Control

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

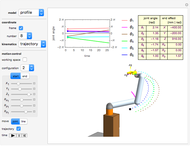
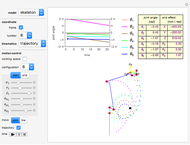
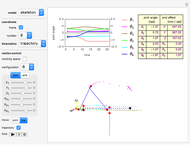
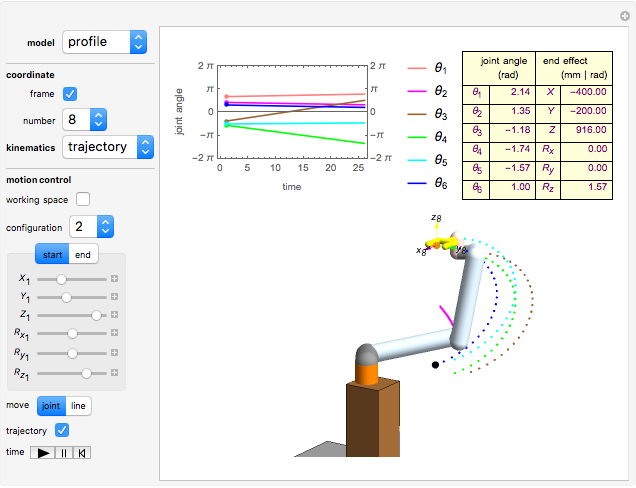
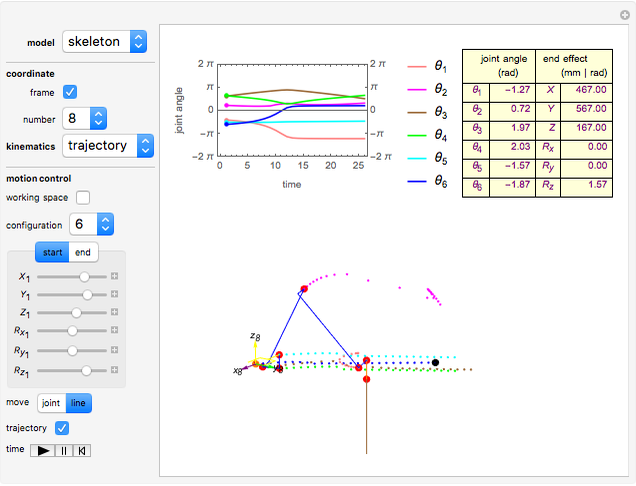
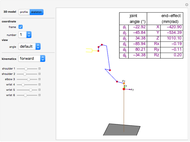
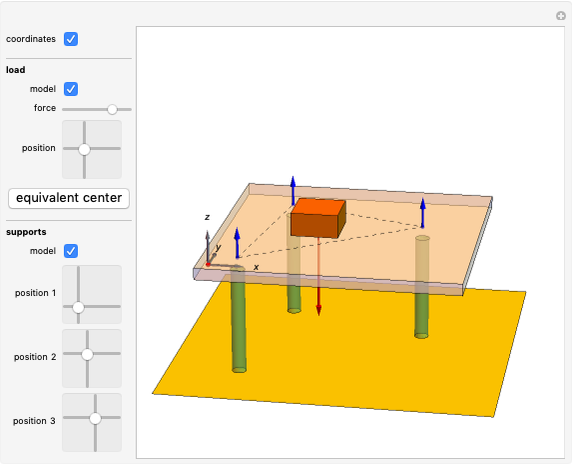
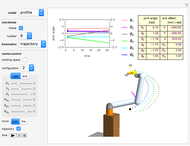
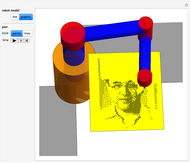
This Demonstration shows the move-joint and move-line methods that are used to control the manipulator trajectory of an industrial robot.

[more]

The move-joint method determines the initial and final poses of the planned trajectory, using inverse kinematics. All joint angles move linearly in the joint space (top-left plot). The trajectory of the end effector or tooling center point (TCP) moves along curves in the 3D tooling space (bottom plot).

The move-line method determines all of the end effector or tooling points from the initial and final poses, along a straight line, by inverse kinematics. The trajectory of the TCP moves linearly in the 3D tooling space (bottom plot), but all joint angles do not move linearly in the joint space (top-left plot).

[less]

Contributed by: Frederick Wu (September 2016)
Open content licensed under CC BY-NC-SA

Snapshots

Details

References

[1] J. Denavit and R. S. Hartenberg, “A Kinematic Notation for Lower-Pair Mechanisms Based on Matrices,” Journal of Applied Mechanics, 22(2), 1955 pp. 215–221.

[2] H. Lipkin, “A Note on Denavit–Hartenberg Notation in Robotics,” in ASME 2005 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Long Beach, CA, 2005. New York: American Society of Mechanical Engineers, 2005. doi:10.1115/DETC2005-85460.

[3] J. J. Craig, Introduction to Robotics: Mechanics and Control, 3rd ed., Upper Saddle River, NJ: Pearson/Prentice Hall, 2005 pp. 62–82.

[4] B. Siciliano and O. Khatib, eds., Springer Handbook of Robotics, Berlin: Springer–Verlag, 2008.

[5] B. Siciliano, L. Sciavicco, L. Villani and G. Oriolo, Robotics: Modelling, Planning and Control, London: Springer, 2009.

[6] D. L. Pieper, “The Kinematics of Manipulators under Computer Control,” (Stanford Artificial Intelligence Laboratory Memo, No. AI-72), Ph.D. dissertation, Computer Science Department, School of Humanities and Sciences, Stanford University, CA, 1968. www.dtic.mil/cgi-bin/GetTRDoc?AD=AD0680036.

[7] M. Raghavan and B. Roth, “Kinematic Analysis of the 6R Manipulator of General Geometry,” in Proceedings of the Fifth International Symposium on Robotics Research (H. Miura, ed.), Cambridge, MA: MIT Press, 1990 pp. 263–269. dl.acm.org/citation.cfm?id=112715&CFID=542850644&CFTOKEN=11490130.

[8] D. Manocha and J. F. Canny, “Efficient Inverse Kinematics for General 6R Manipulators,” IEEE Transactions on Robotics and Automation, 10(5), 1994 pp. 648–657. doi:10.1109/70.326569.

[9] R. N. Jazar, Theory of Applied Robotics: Kinematics Dynamics and Control, 2nd ed., New York: Springer, 2010 pp. 341–363.

[10] UR10/CB3 User Manual, Version 3.1, Denmark Odense: Universal Robots A/S, 2015. (Aug 26, 2016) www.universal-robots.com/media/8755/ur10_user_manual _da _global.pdf.

[11] The URScript Programming Language, Version 3.1, Denmark Odense: Universal Robots A/S, 2015. (Aug 26, 2016) www.sysaxes.com/manuels/scriptmanual_en_ 3.1.pdf.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send