Joule (Free) Expansion Based on a Block Cellular Automaton

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
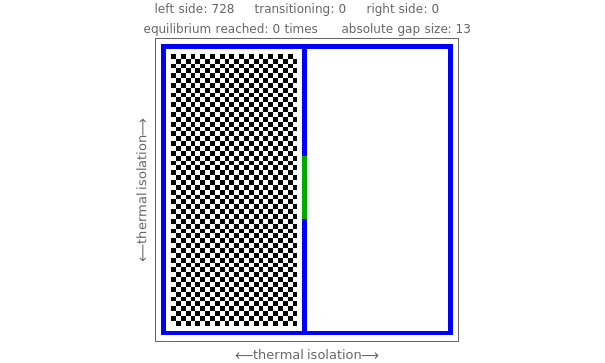
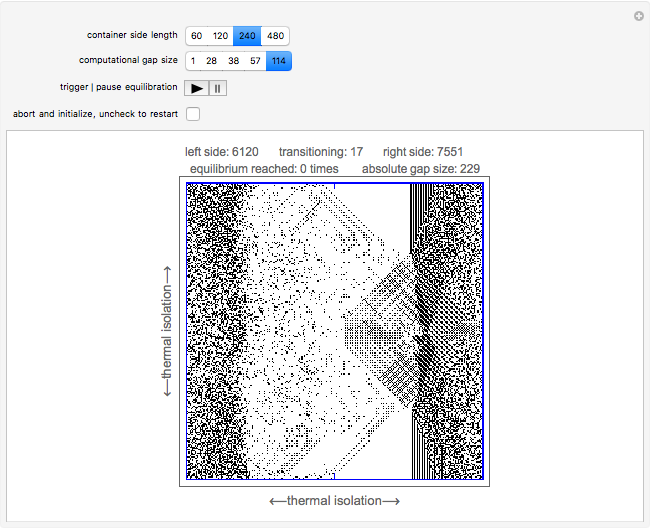
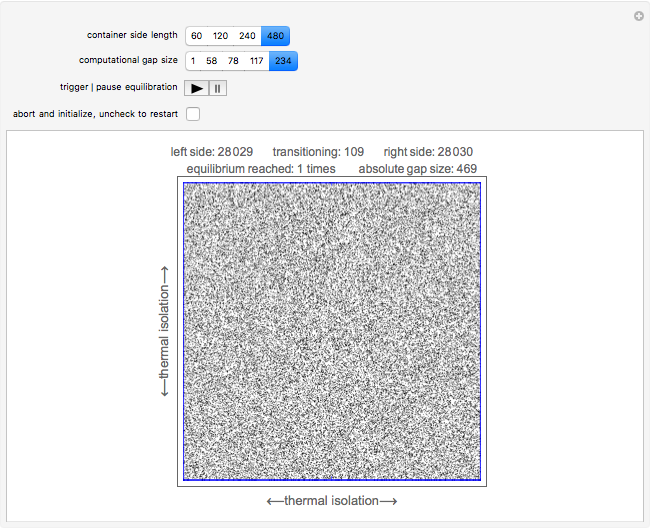
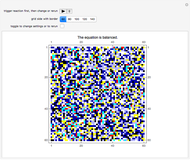
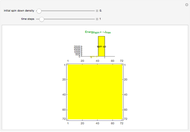
In this Demonstration a rigid square container is divided into two compartments of equal volume separated by a rigid dividing barrier with an adjustable gap in the middle. The container is thermally isolated from its surroundings. At startup, the left compartment contains an ideal gas exerting a pressure 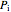 and the right compartment is evacuated. The gas expands to fill the entire two-compartment volume by way of collision-driven particle transfer between the two compartments. Moreover, the expansion proceeds ultimately to equalize the pressure on the two sides of the dividing barrier. Turbulence is evident at many places in both compartments as the expansion proceeds.
and the right compartment is evacuated. The gas expands to fill the entire two-compartment volume by way of collision-driven particle transfer between the two compartments. Moreover, the expansion proceeds ultimately to equalize the pressure on the two sides of the dividing barrier. Turbulence is evident at many places in both compartments as the expansion proceeds.
Contributed by: Michael Dewus (October 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The plot label keeps track of the current absolute gap size in accord with the following details concerning gap size. The maximum allowable gap size in gas particle units for a given container side length is calculated as  , where
, where  is container side length—arbitrary computational gap sizes
is container side length—arbitrary computational gap sizes  for a given
for a given  are shown in the plot label setter bar, where the rightmost setting is the maximum allowable. For each computational gap size
are shown in the plot label setter bar, where the rightmost setting is the maximum allowable. For each computational gap size  , there is an absolute gap size that corresponds to the green segment in the gap seen in the plot; these absolute gap sizes are calculated as
, there is an absolute gap size that corresponds to the green segment in the gap seen in the plot; these absolute gap sizes are calculated as 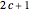 . If allowable gap size maxima are exceeded, the absolute gap size defaults to 3. The code uses the previously set gap size if possible when you switch to a different
. If allowable gap size maxima are exceeded, the absolute gap size defaults to 3. The code uses the previously set gap size if possible when you switch to a different  —in this way you can make use of the available gap sizes of other container side lengths.
—in this way you can make use of the available gap sizes of other container side lengths.
The computation is based on a 2×2 block cellular automaton (BCA). The primary function of the BCA is to simulate the random collisions that catalyze the gaseous particle transfer between the compartments. The BCA uses 16 rules that deflect all manner of collision scenarios—pictograms of these rules may be obtained as explained in the code. BCA feedback of rule-based updating (information feedback and dynamic refresh) is the key operative that drives and sustains the gas dynamics.
You will notice an apparent spin behavior when particles recoil off the barriers; it is a function of the combined effects of BCA rotation subsequent to rule application and the influence of feedback.
The plot label counts equilibrium events and compartment totals as well as particles transitioning between compartments. You can use the abort checkbox at any time to change the container settings or to initialize and restart expansion—be sure to uncheck this control to restart; also use this control to force various forms of left compartment jettisons.
Brief physics background: the first law of thermodynamics requires that 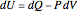 , following the sign convention that heat
, following the sign convention that heat 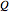 is positive when it enters a system (a "deposit" into the system's internal energy "bank") and negative when it leaves (a "withdrawal"); work
is positive when it enters a system (a "deposit" into the system's internal energy "bank") and negative when it leaves (a "withdrawal"); work  is positive when it leaves a system (a "withdrawal") and negative when it enters (a "deposit");
is positive when it leaves a system (a "withdrawal") and negative when it enters (a "deposit"); 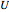 is the system's internal energy "bank". In the classical approach to free expansion according to the first law,
is the system's internal energy "bank". In the classical approach to free expansion according to the first law, 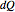 is zero because the entire system is thermally isolated, and
is zero because the entire system is thermally isolated, and 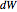 is zero because the system's volume remains constant (i.e., no negative or positive work is done on or by the system). This means that for such a system
is zero because the system's volume remains constant (i.e., no negative or positive work is done on or by the system). This means that for such a system 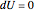 , and since for an ideal gas the internal energy
, and since for an ideal gas the internal energy 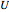 is a function of temperature alone,
is a function of temperature alone,  must be zero. Where
must be zero. Where 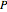 is pressure,
is pressure,  is volume,
is volume,  is moles of gas,
is moles of gas, 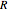 is the universal gas constant, and
is the universal gas constant, and  is temperature, since the system's temperature remains constant, it follows from the ideal gas law (
is temperature, since the system's temperature remains constant, it follows from the ideal gas law (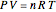 ) that
) that 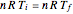 , or,
, or, 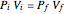 .
.
Since the gas originally occupied the left compartment volume 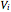 , and finally filled both compartments' volume
, and finally filled both compartments' volume 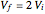 , it must hold that
, it must hold that 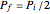 , which is what the nonclassical BCA approach shows—that is, when the pressure on the dividing barrier equilibrates, the gaseous particle count in the left compartment exactly halves, which is tantamount to saying that the pressure also halves. And as the gaseous particle count in the right compartment shows, the pressure there is
, which is what the nonclassical BCA approach shows—that is, when the pressure on the dividing barrier equilibrates, the gaseous particle count in the left compartment exactly halves, which is tantamount to saying that the pressure also halves. And as the gaseous particle count in the right compartment shows, the pressure there is 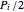 as well; thus the final pressure in the container is everywhere
as well; thus the final pressure in the container is everywhere 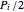 , as expected from the classical approach to the problem. Also, limited experimentation shows that once the BCA equilibrates the pressure on the dividing barrier, the system appears to remain in that state within small statistical deviations. That is to say, computational equilibrium appears to have been realized. The third snapshot shows the system having achieved equilibrium once for the largest container side length and and its largest gap size—you can trigger this snapshot to test the tenacity of the equilibrium state.
, as expected from the classical approach to the problem. Also, limited experimentation shows that once the BCA equilibrates the pressure on the dividing barrier, the system appears to remain in that state within small statistical deviations. That is to say, computational equilibrium appears to have been realized. The third snapshot shows the system having achieved equilibrium once for the largest container side length and and its largest gap size—you can trigger this snapshot to test the tenacity of the equilibrium state.
References
[1] B. Chopard and M. Droz, Cellular Automata Modeling of Physical Systems, Cambridge: Cambridge University Press, 2005.
[2] M. W. Zemansky, Heat and Thermodynamics, New York: McGraw-Hill, 1957.
[3] Wikipedia, "Joule Expansion." (Jul 20, 2012) en.wikipedia.org/wiki/Joule_expansion.
[4] Wikipedia, "Ideal Gas." (Sep 25, 2012) en.wikipedia.org/wiki/Ideal_gas.
[5] Wikipedia, "James Prescott Joule." (Oct 6, 2012) en.wikipedia.org/wiki/James_Joule.
[6] Wikipedia, "Monatomic Gas." (Oct 17, 2012) en.wikipedia.org/wiki/Monatomic_gas.
[7] Wikipedia, "Pressure." (Oct 22, 2012) en.wikipedia.org/wiki/Pressure.
[8] Wikipedia, "Negative Feedback." (Mar 8, 2013)en.wikipedia.org/wiki/Negative_feedback.
[9] Wikipedia, "Positive Feedback." (Mar 8, 2013)en.wikipedia.org/wiki/Positive_feedback.
Permanent Citation