Kakutani's Solution of the Dirichlet Problem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
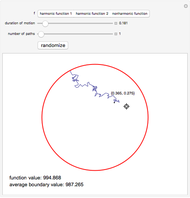
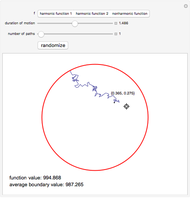
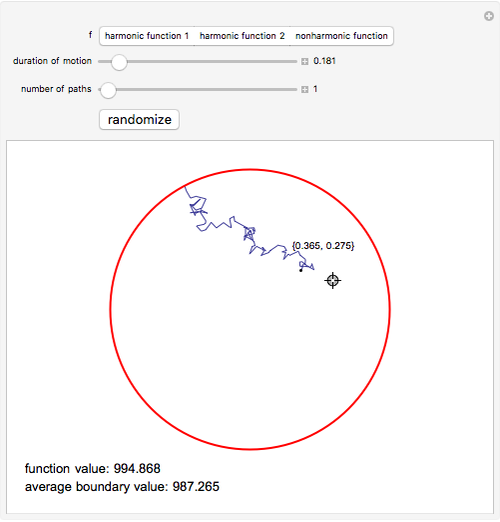
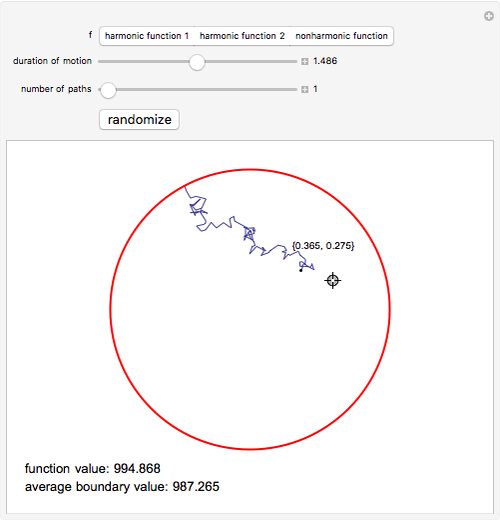
Choose one of the three functions using the setter bar. Move the locator to a point in the unit circle. You will see the value of the selected function at this point displayed below the circle. Now increase the duration of motion. A Brownian path will emerge from the chosen point. Keep increasing the duration until the Brownian path hits the boundary of the circle. The value of the chosen function at the point where the path hits the boundary will appear below the value of the function at the point from which the path emerged. Now increase the number of paths, increasing the time duration, if necessary, to make sure they all hit the boundary. If the selected function is harmonic (the first and second choices), the average of the values of the function at the points where the Brownian paths hit the boundary will converge to the value of the function at the starting point of the path. If the selected function is not harmonic (the third choice), the average will converge to the value of a different (harmonic) function that coincides with the given function on the boundary.
Contributed by: Andrzej Kozlowski (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A function of two variables 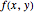 is called harmonic if it is a solution of the Laplace equation
is called harmonic if it is a solution of the Laplace equation 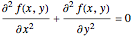 . An example of a harmonic function is the real or the imaginary part of a complex analytic function viewed as a function of two real variables. The Dirichlet problem in two dimensions is this: given a reasonable domain in
. An example of a harmonic function is the real or the imaginary part of a complex analytic function viewed as a function of two real variables. The Dirichlet problem in two dimensions is this: given a reasonable domain in 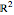 and a continuous function
and a continuous function  on its boundary, find a smooth function
on its boundary, find a smooth function  that coincides with
that coincides with 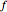 on the boundary and is harmonic in the interior of the region. In 1944 Kakutani showed that the solution can be expressed in term of Brownian motion. This Demonstration illustrates the Kakutani construction for the case of the unit disc. You can choose one of three functions using the setter bar. The first two are harmonic, the third one is not. The harmonic functions are given by the formulas
on the boundary and is harmonic in the interior of the region. In 1944 Kakutani showed that the solution can be expressed in term of Brownian motion. This Demonstration illustrates the Kakutani construction for the case of the unit disc. You can choose one of three functions using the setter bar. The first two are harmonic, the third one is not. The harmonic functions are given by the formulas 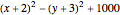 and
and 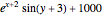 . The nonharmonic function is a polynomial of degree five with positive coefficients.
. The nonharmonic function is a polynomial of degree five with positive coefficients.
Permanent Citation
"Kakutani's Solution of the Dirichlet Problem"
http://demonstrations.wolfram.com/KakutanisSolutionOfTheDirichletProblem/
Wolfram Demonstrations Project
Published: March 7 2011