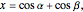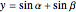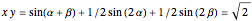Kempe's Universality Theorem: An Example

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
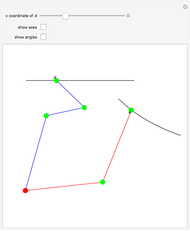
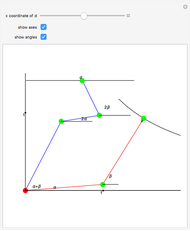
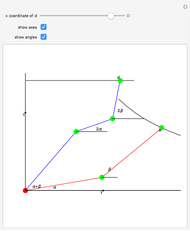
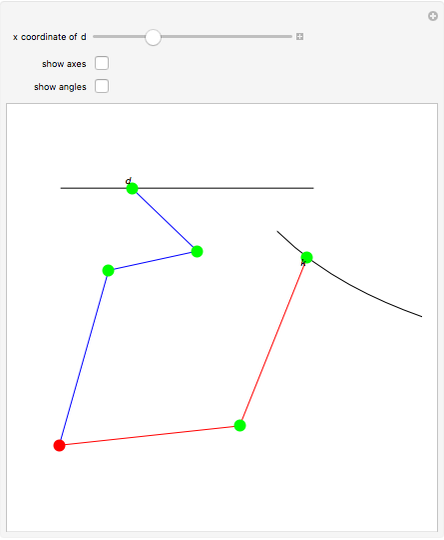
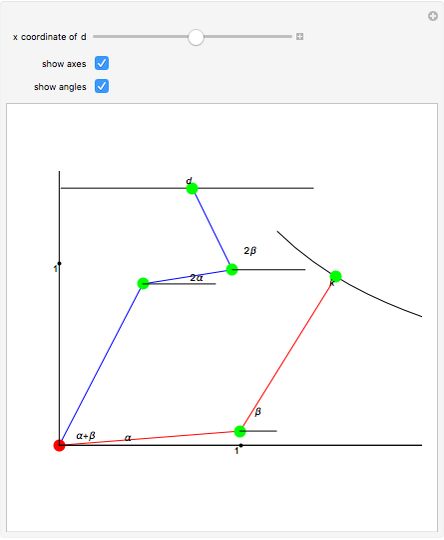
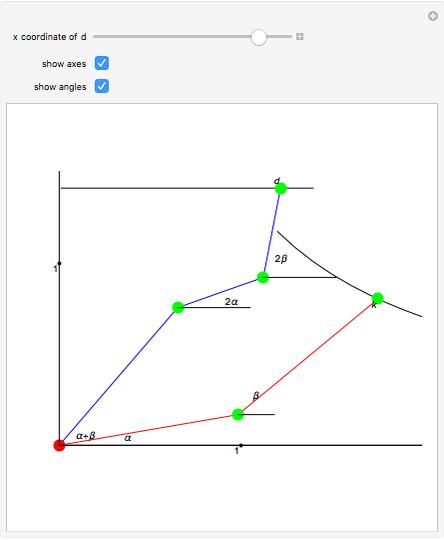
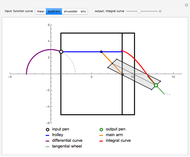
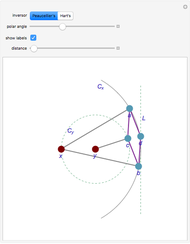
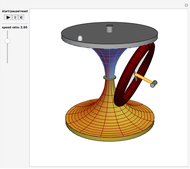
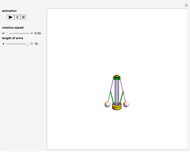
Roughly, Kempe's universality theorem states that any finite part of a plane algebraic curve can be traced out by a vertex of some linkage. This Demonstration illustrates a particular example: there exists a linkage such that, if the point  is forced to move on the straight line
is forced to move on the straight line  , the point
, the point  moves on the hyperbola
moves on the hyperbola 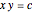 .
.
Contributed by: Izidor Hafner (August 2008)
Based on description given by: Erik D. Demaine and Joseph O'Rourke
Open content licensed under CC BY-NC-SA
Snapshots
Details
E. D. Demaine and J. O'Rourke, Geometric Folding Algorithms: Linkages, Origami, Polyhedra, New York: Cambridge University Press, 2007 pp. 31–36.
Permanent Citation