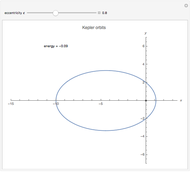
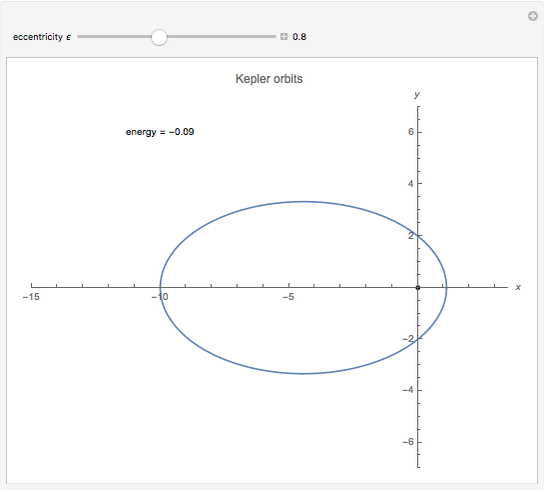
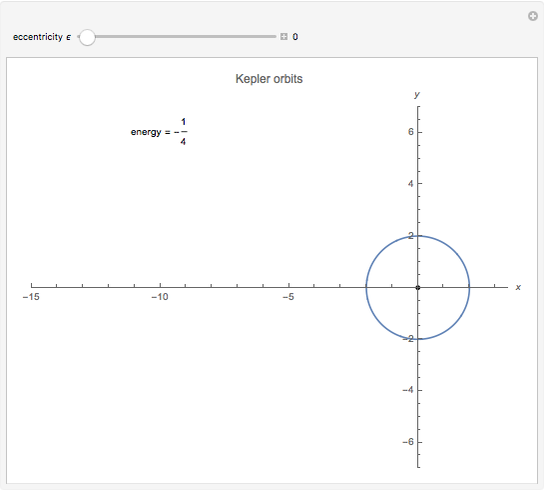
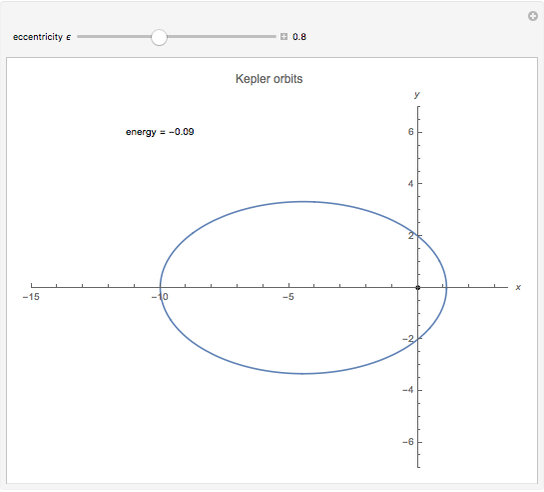
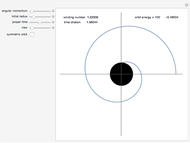
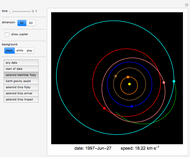
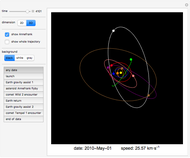
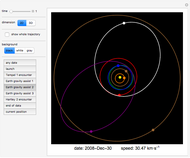
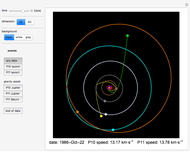
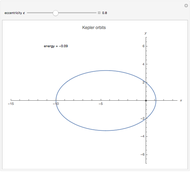
The Kepler orbits for a two-body system under a central gravitational force can be represented by a polar curve that relates the distance between the two bodies with the angle from the axis. The shape of the orbit depends on its eccentricity, which is determined by the energy of the system.