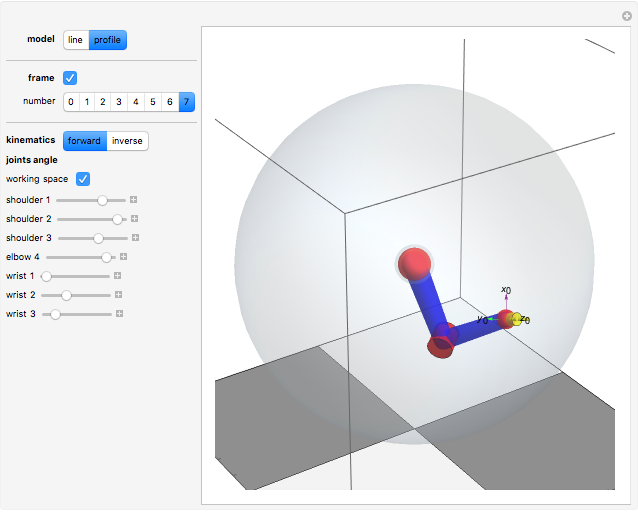
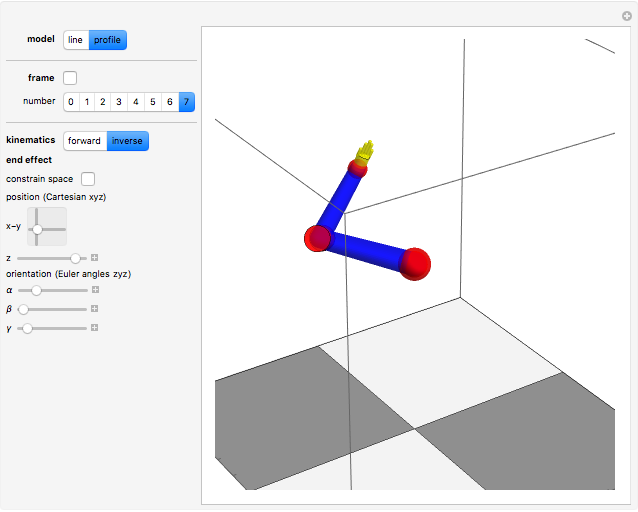
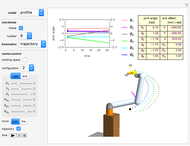
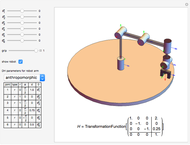
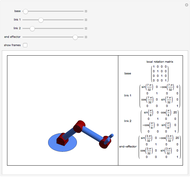
Kinematics of a Redundant Anthropomorphic Arm with Seven Degrees of Freedom

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
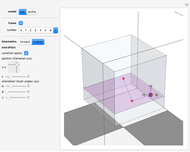
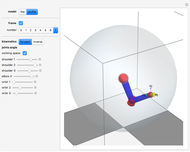
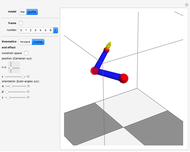
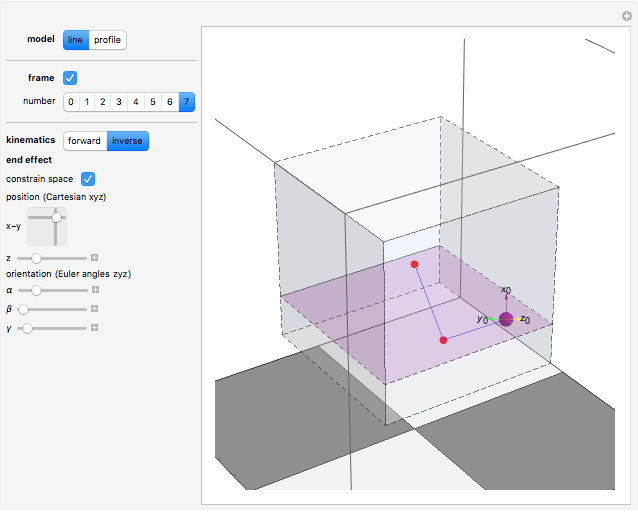
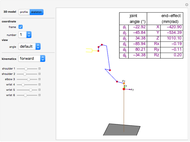
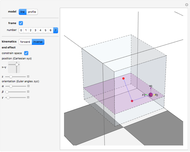
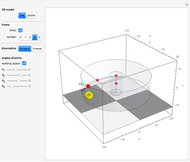
The anthropomorphic arm with seven degrees of freedom (DoF) includes redundancy, since the number of joints ( ) is greater than the dimension of the manipulation variables, which have three position coordinates and three orientation angles (
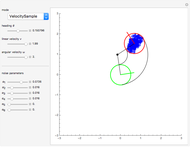
) is greater than the dimension of the manipulation variables, which have three position coordinates and three orientation angles ( ). Although the set of nonlinear trigonometric equations cannot typically be solved analytically, there are some robot structures that are solvable analytically. Pieper proposed a decoupling method [1]; the sufficient condition for solvability is when the 6-DoF robot has three consecutive revolute joints with axes intersecting in one point. Another generalized inverse is the inertiaâ€Âweighted pseudoinverse Jacobian matrix, a kind of resolved motion rate control technique, proposed by Whitney [2], which is used to minimize energy by using the inertia matrix as the weighting matrix.
). Although the set of nonlinear trigonometric equations cannot typically be solved analytically, there are some robot structures that are solvable analytically. Pieper proposed a decoupling method [1]; the sufficient condition for solvability is when the 6-DoF robot has three consecutive revolute joints with axes intersecting in one point. Another generalized inverse is the inertiaâ€Âweighted pseudoinverse Jacobian matrix, a kind of resolved motion rate control technique, proposed by Whitney [2], which is used to minimize energy by using the inertia matrix as the weighting matrix.
Contributed by: Frederick Wu (November 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] D. L. Pieper, "The Kinematics of Manipulators under Computer Control," (Stanford Artificial Intelligence Laboratory Memo, No. AI-72), Ph.D. dissertation, Computer Science Department, School of Humanities and Sciences, Stanford University, CA, 1968. www.dtic.mil/cgi-bin/GetTRDoc?AD=AD0680036.
[2] D. E. Whitney, "Resolved Motion Rate Control of Manipulators and Human Prostheses," IEEE Transactions on Man-Machine Systems, 10(2), 1969 pp. 47–53. doi:10.1109/TMMS.1969.299896.
[3] B. Siciliano, L. Sciavicco, L. Villani, and G. Oriolo, Robotics: Modelling, Planning and Control, London: Springer-Verlag, 2009 pp. 39–160.
[4] R. N. Jazar, Theory of Applied Robotics: Kinematics, Dynamics, and Control, 2nd ed., New York: Springer-Verlag, 2010 pp. 357–363.