Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Kinematics of Planar Elastic Chains

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

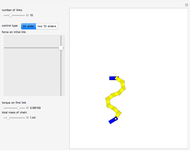
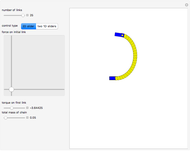
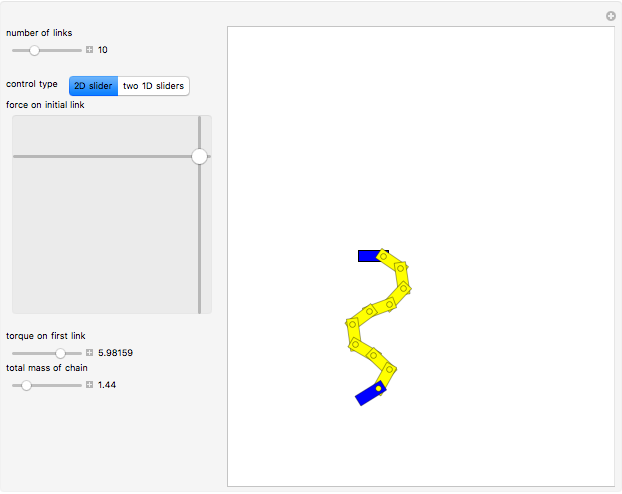
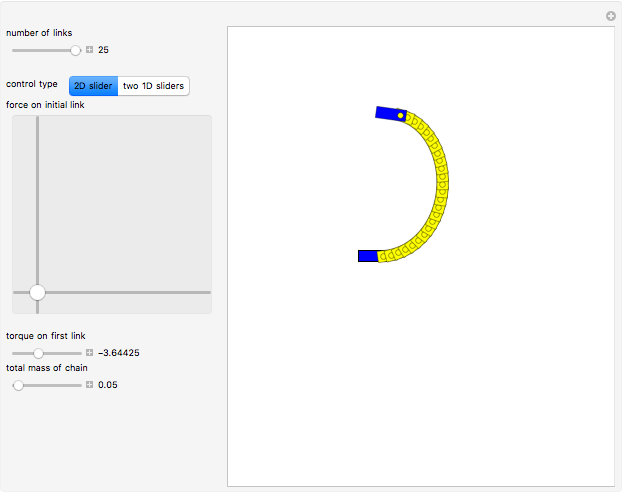
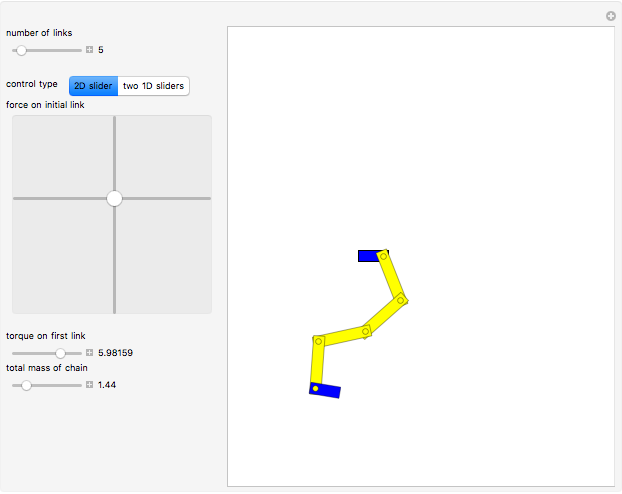
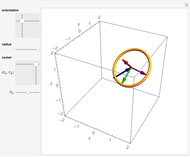
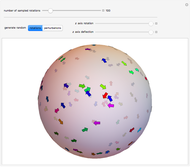
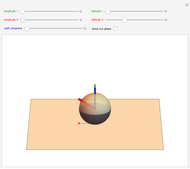
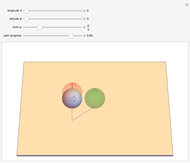
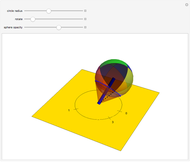
This Demonstration shows an -link planar kinematic chain with a fixed base in which each joint is a linearly elastic torsional spring. The shape of this chain in static equilibrium can be represented as the solution of a discrete-time optimal control problem, with boundary conditions that vary with the position and orientation of the last link. McCarthy and Bretl proved that the set of all solutions to this problem is a smooth manifold that can be parameterized by a single chart. We have added gravitational force to this model.

Contributed by: Rose Morris-Wright and Aaron Becker (August 2012)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Given a fixed position for the left end of the chain (shown in blue), equilibrium configurations can be obtained by minimizing the equation of potential energy. In this minimization process, we obtain costate vectors (similar to Lagrange multipliers) and we find that there is a diffeomorphism between the initial costate vectors and the space of nonsingular equilibrium configurations [1]. The initial constants can also be interpreted as the force and torque of the first (yellow) link on the initial (blue) link.

Reference

[1] Z. McCarthy and T. Bretl, "Mechanics and Manipulation of Planar Elastic Kinematic Chains," in Proceedings of the 2012 IEEE International Conference on Robotics and Automation (ICRA12), St. Paul, Minn., IEEE, 2012 pp. 2798–2805.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send