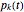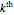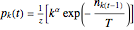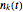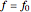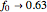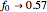Kolkata Paise Restaurant (KPR) Problem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
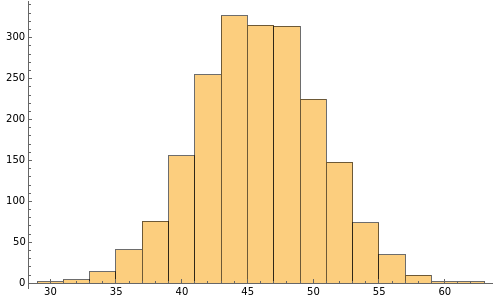
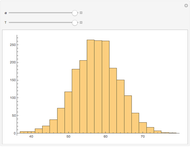
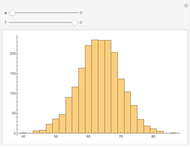
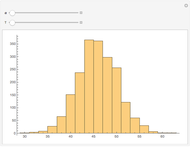
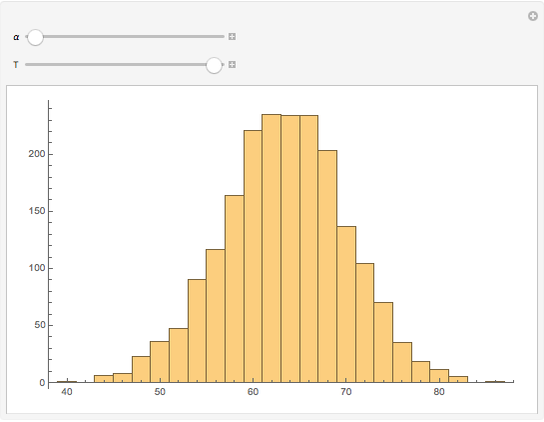
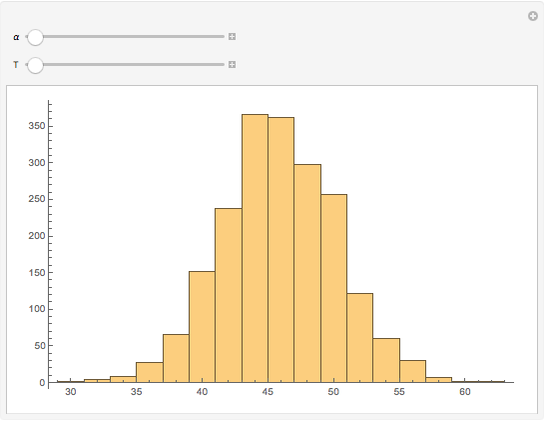
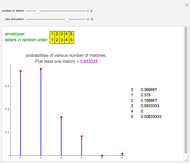
The KPR problem is a repeated game, played between a large number of agents having no interaction among themselves. In KPR, 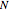 prospective customers (the agents) choose from
prospective customers (the agents) choose from 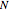 restaurants each evening (time
restaurants each evening (time  ) in parallel decision mode. Each restaurant has the same price for a meal but a different rank
) in parallel decision mode. Each restaurant has the same price for a meal but a different rank  (agreed upon by all the customers) and can serve only one customer. If more than one customer arrives at any restaurant on any evening, one of them is randomly chosen and is served and the rest do not get dinner that evening. Information regarding the customer distributions for earlier evenings is available to everyone. Each evening, each customer chooses a restaurant independent of the others. Each customer wants to go to the restaurant with the highest possible rank while avoiding a crowd so as to be able to get dinner there.
(agreed upon by all the customers) and can serve only one customer. If more than one customer arrives at any restaurant on any evening, one of them is randomly chosen and is served and the rest do not get dinner that evening. Information regarding the customer distributions for earlier evenings is available to everyone. Each evening, each customer chooses a restaurant independent of the others. Each customer wants to go to the restaurant with the highest possible rank while avoiding a crowd so as to be able to get dinner there.
Contributed by: Asim Ghosh (Saha Institute of Nuclear Physics, Kolkata, India) and Bikas K. Chakrabarti (Saha Institute Nuclear Physics & Indian Statistical Institute, Kolkata, India) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For more information, see:
A. S. Chakrabarti, B. K. Chakrabarti, A. Chatterjee, and M. Mitra, "The Kolkata Paise Restaurant Problem and Resource Utilization," Physica A 388, 2009 pp. 2420–2426.
A. Ghosh, A. S. Chakrabarti, and B. K. Chakrabarti, "Kolkata Paise Restaurant Problem in Some Uniform Learning Strategy Limits."
Permanent Citation