Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Kowalewski's Settlement Problem for the Rhombic Dodecahedron

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

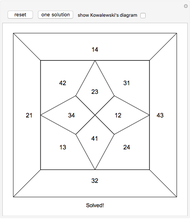
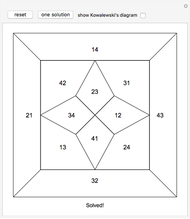
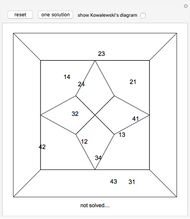
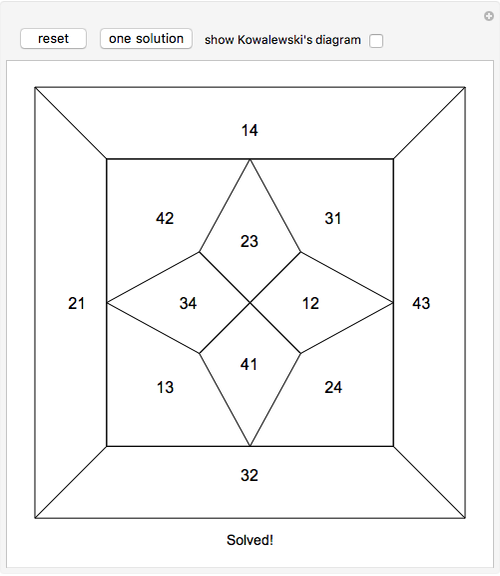
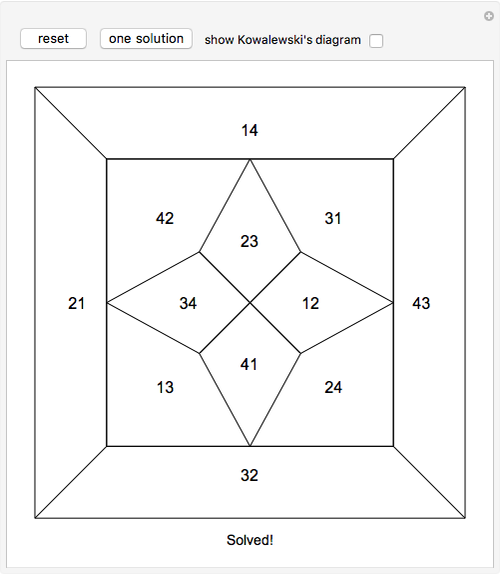
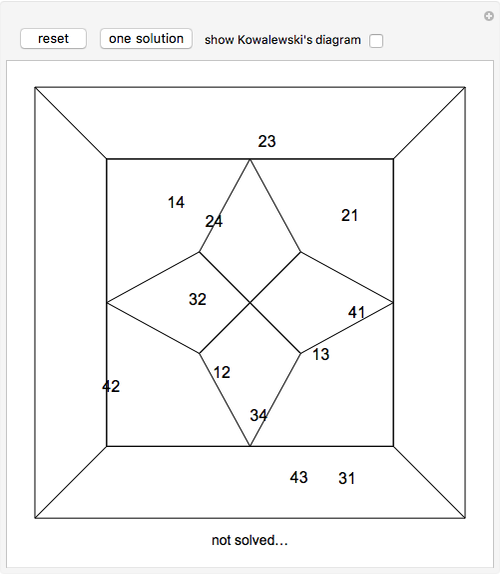
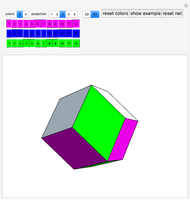
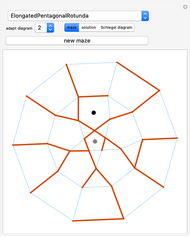
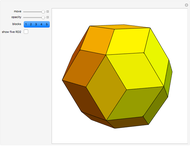
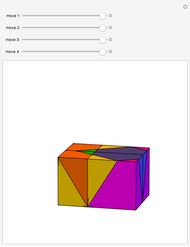
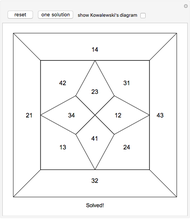
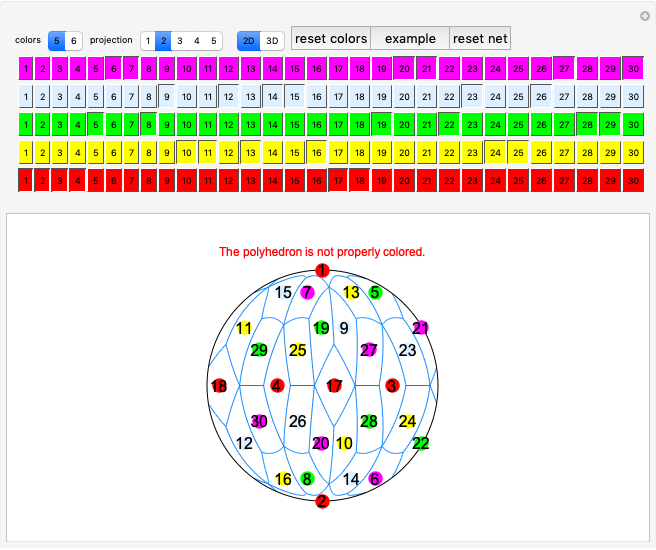
Kowalewski's diagram consists of 12 non-overlapping simply connected regions. Each region has four neighboring regions. There are also 12 two-digit labels. The Kowalewski settlement problem is to place the labels on the regions so that the labels of neighboring regions have exactly one common digit.

Contributed by: Izidor Hafner (August 2019)
Open content licensed under CC BY-NC-SA

Details

Kowalewski's original condition is a little stronger. Two opposing neighboring labels must match the first digit and the other two the second digit. But if a solution with a weak condition is obtained, a solution with a stronger condition can be obtained by swapping some labels by exchanging the digits (e.g. 42 and 24).

Reference

[1] G. Kowalewski and D. Booth, "Construction Games with Kepler's Solid," Austin, TX: Parker Courtney Press, 2001. (Jul 16, 2019) www.zometool.com/content/KowalewskiWeb.pdf.

Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send