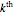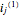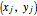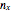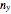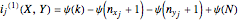Kraskov (KSG) Estimator of Mutual Information

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
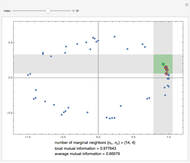
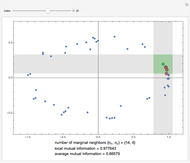
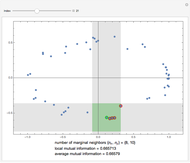
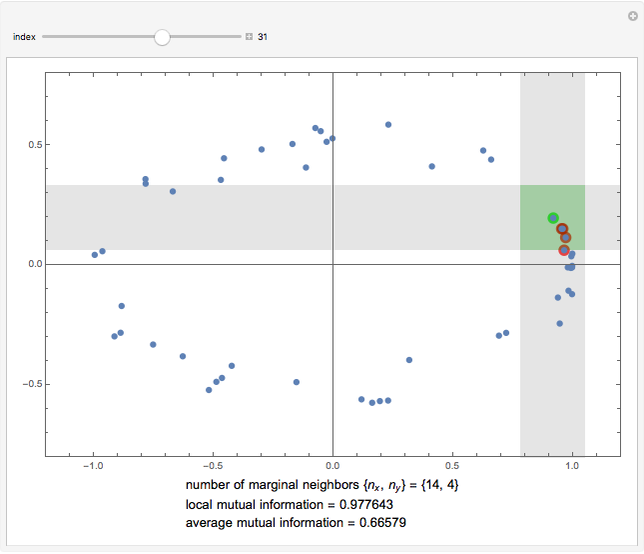
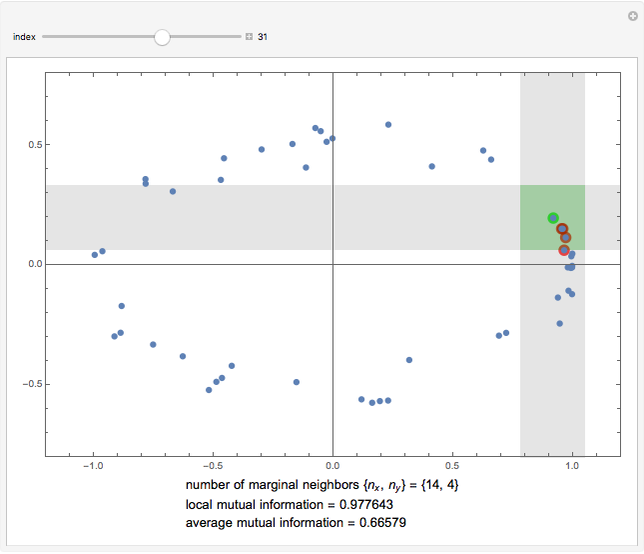
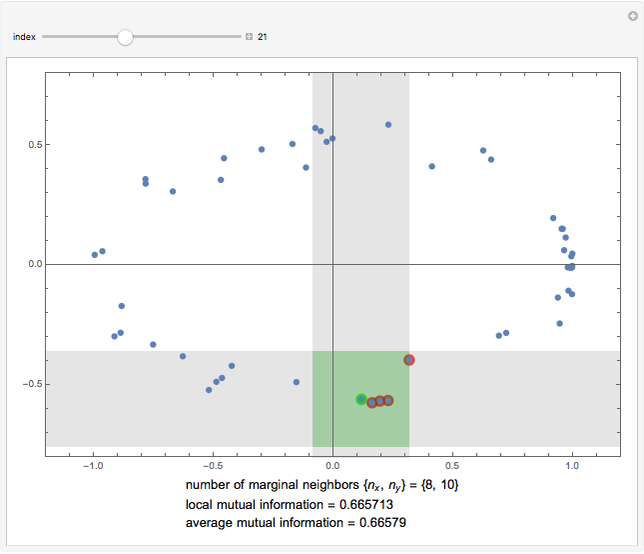
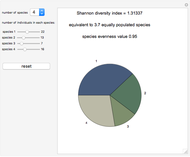
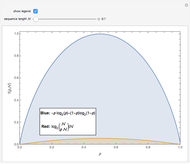
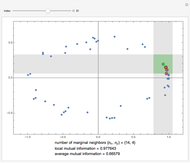
This Demonstration illustrates the operation of the Kraskov–Stögbauer–Grassberger (KSG) estimator [1] of mutual information on a small dataset with a nonlinear dependence structure, which cannot be captured by the Pearson correlation coefficient.
[more]
Contributed by: Leonardo Novelli (August 2018)
Open content licensed under CC BY-NC-SA
Details
References
[1] A. Kraskov, H. Stögbauer and P. Grassberger, "Estimating Mutual Information," Physical Review E, 69(6), 2004. doi:10.1103/PhysRevE.69.066138.
[2] J. T. Lizier, "JIDT: An Information-Theoretic Toolkit for Studying the Dynamics of Complex Systems," Frontiers in Robotics and AI, 1, 2014. doi:10.3389/frobt.2014.00011.
Snapshots
Permanent Citation